
Linear Algebra
&
Engineering Mathematics 1
Week 7 - Matrices
Augmented matrix system - solving a set of equations
- Recall the system of equations that we considered last week: \[ \begin{array}{r} x& +&y&+&z&=&4 \\ x& -&y&-&2z &=& 1 \\ 2x&+& y& -&z &=& 2 \\ \end{array} \]
- Rewrite as a matrix equation:
\(A \mathbf x = \) \( \left( \begin{array}{r} 1 & 1 & 1 \\ 1 & -1 & -2 \\ 2 & 1 & -1 \\ \end{array} \right) \) \( \left( \begin{array}{c} x \\ y \\ z \\ \end{array} \right) \) \( = \left( \begin{array}{c} 4 \\ 1 \\ 2 \\ \end{array} \right) \) \( = \mathbf b \)
Augmented matrix system - solving a set of equations
- Rewrite as a matrix equation:
\(A \mathbf x = \) \( \left( \begin{array}{r} 1 & 1 & 1 \\ 1 & -1 & -2 \\ 2 & 1 & -1 \\ \end{array} \right) \) \( \left( \begin{array}{c} x \\ y \\ z \\ \end{array} \right) \) \( = \left( \begin{array}{c} 4 \\ 1 \\ 2 \\ \end{array} \right) \) \( = \mathbf b \)
- Augmented form:
\( \left( \begin{array}{r|r} A & \mathbf b \end{array} \right) \) = \( \left( \begin{array}{r} \\ \\ \\ \end{array} \right. \) \( \left. \begin{array}{rrr|} 1 & 1 & 1 \;\;\\ 1 & -1 & -2\;\; \\ 2 & 1 & -1 \;\; \\ \end{array} \right. \) \( \left. \begin{array}{r} \;4\\ \;1\\ \;2 \\ \end{array} \right. \) \( \left. \begin{array}{r} \\ \\ \\ \end{array} \right) \)
Augmented matrix system - solving a set of equations
\( \left( \begin{array}{r|r} A & \mathbf b \end{array} \right) \) = \( \left( \begin{array}{r} \\ \\ \\ \end{array} \right. \) \( \left. \begin{array}{rrr|} 1 & 1 & 1 \;\;\\ 1 & -1 & -2\;\; \\ 2 & 1 & -1 \;\; \\ \end{array} \right. \) \( \left. \begin{array}{r} \;4\\ \;1\\ \;2 \\ \end{array} \right. \) \( \left. \begin{array}{r} \\ \\ \\ \end{array} \right) \)
- We can perform a method of elimination by
- Swapping,
- scaling, and/or
- adding rows together.
This method is known as row reduction, Gaussian elimination, Gauss-Jordan elimination.
Problem 1
Let's solve the two problems from last week, which we tackled manually:
a) \(\;\; \begin{array}{r} 3x & + & 5y & = & 2 \\ 2x & - & y & = & 2 \\ \end{array} \)
Recall from last week, solutions are $x = \dfrac{12}{13},$ $y =-\dfrac{2}{13}.$
b) \(\;\; \begin{array}{r} x & + & y & + & z &= & 4 \\ x & - & y & - & 2z & = & 1\\ 2x & + & y & - & z & = & 2 \\ \end{array} \)
Recall from last week, solutions are $x = 4,$ $y =-3,$ $z= 3.$
Visualisation: Gauss-Jordan elimination
The inverse matrix
If $A$ is a square matrix, its inverse matrix $A^{-1}$ satisfies
$AA^{-1} $ $ = A^{-1}A $ $=I.$
Remarks:
- Inverse matrices only exist for square matrices.
- Not every square matrix has an inverse!
- Not every set of simultaneous equations has a solution!
The inverse matrix
If $A$ is a square matrix, its inverse matrxi $A^{-1}$ satisfies
$AA^{-1} $ $ = A^{-1}A $ $=I.$
Why do we need an inverse in practice?
How can we compute the inverse of a matrix?

We will find inverses using augmented matrices!
Checkpoint
Which of these is the inverse matrix of \( \left( \begin{array}{r} 0 & 1 \\ 1 & 0 \end{array} \right) \) ? (How could we check?)
i) \( \left( \begin{array}{r} 0 & 1 \\ 1 & 0 \end{array} \right) \)
ii) \( \left( \begin{array}{r} 1 & 0 \\ 0 & 1 \end{array} \right) \)
iii) \( \left( \begin{array}{r} 0 & 1 & 0 \\ 1 & 0 & 0 \end{array} \right) \)
iv) \( \left( \begin{array}{r} 1 & 0 & 0 \\ 0 & 1 & 0 \end{array} \right) \)
Problem 2
a) Find the inverse matrix of \( \left( \begin{array}{r} 3 & 5 \\ 2 & -1 \\ \end{array} \right), \)
then show that $A^{-1}$ satisfies $AA^{-1} = A^{-1}A = I.$
\[ A^{-1} = \frac{1}{13} \left( \begin{array}{r} 1 & 5 \\ 2 & -3 \\ \end{array} \right) \]
Problem 2
b) Find the inverse matrix of \( \left( \begin{array}{r} 1 & 1 & 1 \\ 1 & -1 & -2 \\ 2 & 1 & -1 \\ \end{array} \right), \)
then show that $A^{-1}$ satisfies $AA^{-1} = A^{-1}A = I.$
\[ A^{-1} = \frac{1}{3} \left( \begin{array}{r} 3 & 2 & -1 \\ -3 & -3 & 3 \\ 3 & 1 & -2 \\ \end{array} \right) \]
Problem 3
Now we can use our inverse to solve
\(\begin{array}{r} x & + & y & + & z &= & 4 \\ x & - & y & - & 2z & = & 1\\ 2x & + & y & - & z & = & 2 \\ \end{array}\)
(recall that $x= 4,$ $ y = -3,$ $z=3$).
$A \mathbf x = \mathbf b$ $\,\Rightarrow\, $ $ \mathbf x = $ $ A^{-1}A\mathbf x = A^{-1}\mathbf b$
Problem 3
Now we can use our inverse to solve
\(\begin{array}{r} x & + & y & + & z &= & 4 \\ x & - & y & - & 2z & = & 1\\ 2x & + & y & - & z & = & 2 \\ \end{array}\)
(recall that $x= 4,$ $ y = -3,$ $z=3$).
$A \mathbf x = \mathbf b$ $\,\Rightarrow\, $ $ \mathbf x = $ $ A^{-1}A\mathbf x = A^{-1}\mathbf b$
$ \mathbf x = A^{-1} \mathbf b$ $ = \frac{1}{3} \left( \begin{array}{r} 3 & 2 & -1 \\ -3 & -3 & 3 \\ 3 & 1 & -2 \\ \end{array} \right) \left( \begin{array}{r} 4 \\ 1 \\ 2 \\ \end{array} \right) $ $ = \left( \begin{array}{r} 4 \\ -3 \\ 3 \\ \end{array} \right) $
Matrix determinant
Is there a way to tell if a square matrix has an inverse?
\[ \text{det}(A) = |A| \neq 0. \]
A matrix with zero determinant has no inverse!
A matrix without an inverse is called a singular matrix or a non-invertible matrix .
Matrix determinant
For a $2\times 2 $ matrix \(\,A = \left( \begin{array}{r} a & b \\ c & d \\ \end{array} \right),\; \) then
\( \text{det}(A) \) \(= \left| \begin{array}{r} a & b \\ c & d \\ \end{array} \right| \) \( = ad - bc. \)
Matrix determinant
For a $3\times 3 $ matrix \(\,A = \left( \begin{array}{r} a & b & c\\ d & e & f\\ g & h & i \end{array} \right),\; \) then
\( \text{det}(A) \) \(= \left| \begin{array}{r} a & b & c\\ d & e & f\\ g & h & i \end{array} \right| \)
\(\qquad \; = a \left| \begin{array}{r} e & f \\ h & i \\ \end{array} \right| \) \( - b \left| \begin{array}{r} b & f \\ g & i \\ \end{array} \right| \) \( + c \left| \begin{array}{r} d & e \\ g & h \\ \end{array} \right| \)
\(\qquad \; = a (e \,i - f\,h ) - b (d\,i - f\,g) + c (d\,h -e\,g) \)
Matrix determinant
Checkpoint
Which of these matrices is non-invertible?
i) \( \left( \begin{array}{r} 0 & 1 \\ 1 & 0 \end{array} \right) \)
ii) \( \left( \begin{array}{r} 1 & 0 \\ 0 & 1 \end{array} \right) \)
iii) \( \left( \begin{array}{r} 0 & 1 & 0 \\ 1 & 0 & 0 \end{array} \right) \)
iv) \( \left( \begin{array}{r} 1 & 0 \\ 0 & 0 \end{array} \right) \)
Problem 4
Find the determinants of
a) \( \left[ \begin{array}{r} 3 & 2 \\ 4 & -1 \end{array} \right] \)
b) \( \left[ \begin{array}{r} 1 & 2 & 3 \\ 1 & -2 & 1 \\ -1 & -2 & 2 \end{array} \right] \)
c) \( \left[ \begin{array}{r} 1 & 2 & 3 \\ 1 & -2 & 1 \end{array} \right] \)
What's next? Eigenvalues and Eigenvectors
Linear systems
|
Determinants
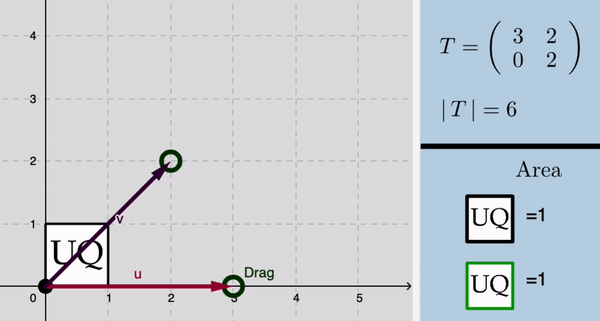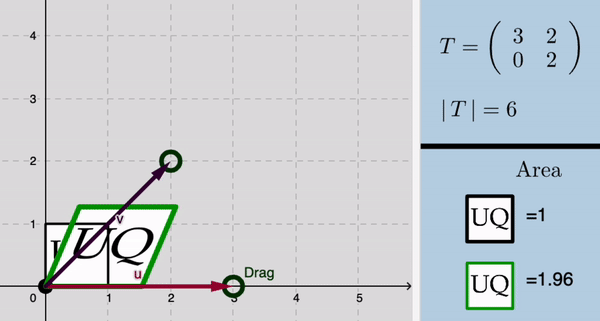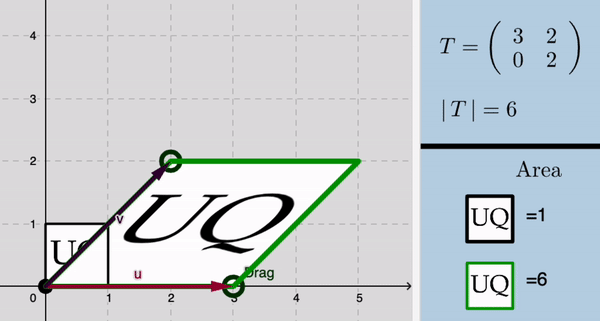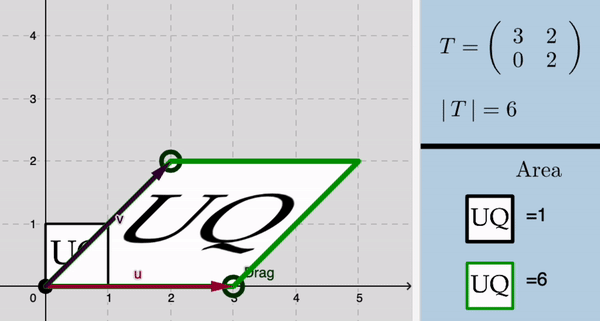
|
|
$\ds T = \left(\begin{matrix} 3 & 1 \\ 1 & 2 \end{matrix}\right) $ |
|
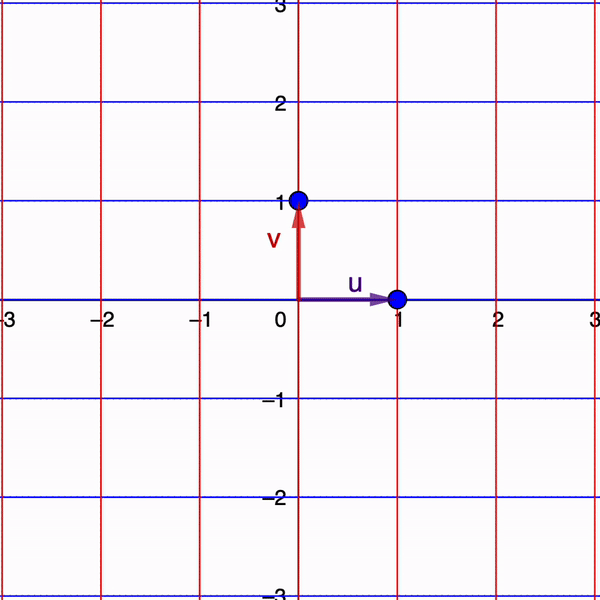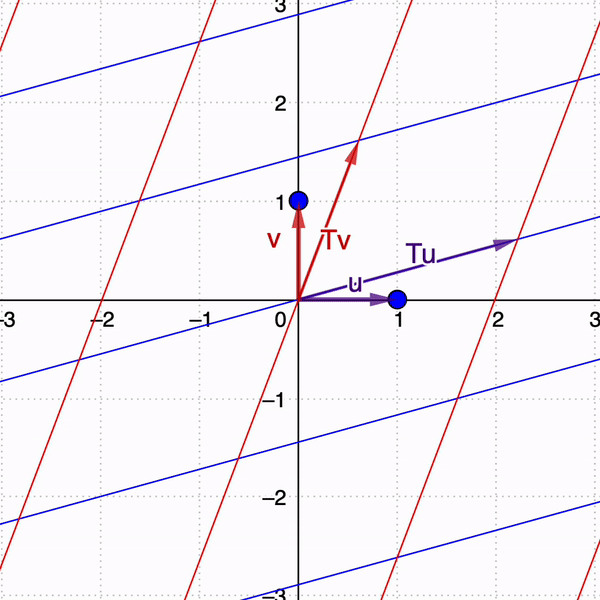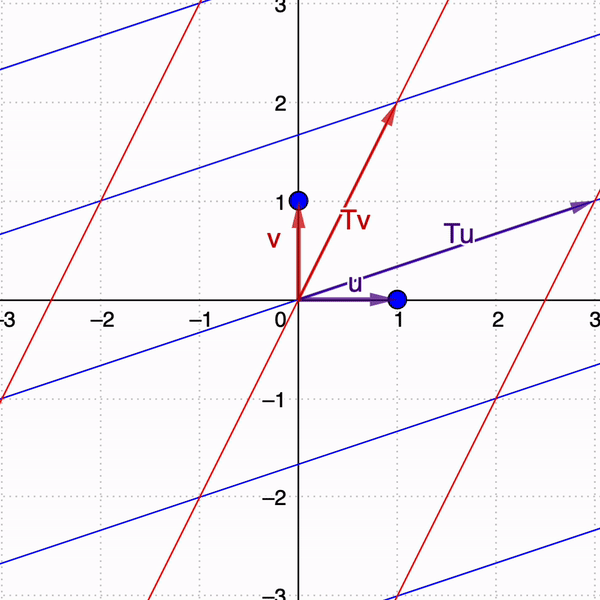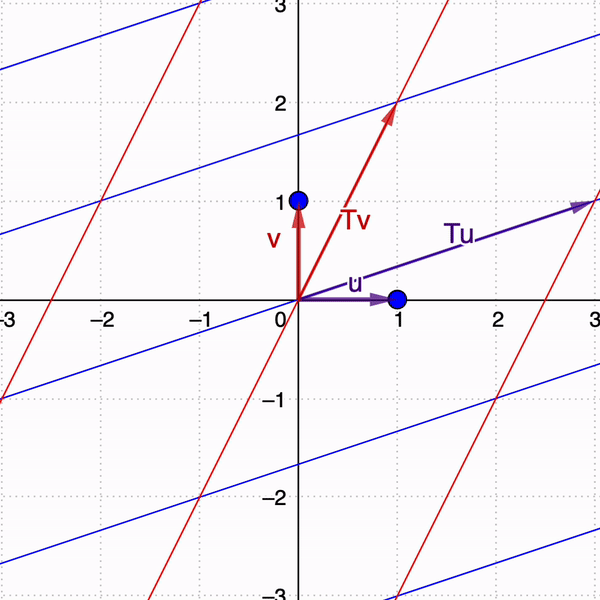
Matrices as Linear transformations
Linear transformation
To begin, consider a linear transformation in two dimensions given by a matrix $A$.
Linear transformation
To begin, consider a linear transformation in two dimensions given by a matrix $A$.
Linear transformation
To begin, consider a linear transformation in two dimensions given by a matrix $A$.
Linear transformation
To begin, consider a linear transformation in two dimensions given by a matrix $A$.
Linear transformation
Considering the matrix $A = \left(\begin{matrix} 3 & 1 \\ 0 & 2 \end{matrix}\right). $
Eigenvalues and Eigenvectors
If $A $ is an $n\times n$ matrix, then $\v$ is an eigenvector if
$A \v $ $ = \lambda \v$
The scalar $\lambda$ is an eigenvalue of $A$, and we say that $\v$ is an eigenvector corresponding to $\lambda.$
Eigenvalues and Eigenvectors
Matrix-vector multiplication $\qquad \qquad$
| $\uparrow$ | ||
| $A\mathbf v $ | $ = $ | $\lambda \v$ |
| $ \downarrow$ |
$\qquad \qquad$ Scalar multiplication
Eigenvalues and Eigenvectors
$A \v = \lambda \v$
to make sense of this equation, consider the $3\times 3$ identity matrix:
$I = \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array}\right) $
Eigenvalues and Eigenvectors
$A \v = \lambda \v$
Multiply by $\lambda$ to obtain:
$\lambda I = \left(\begin{array}{ccc} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda \\ \end{array}\right) $
Eigenvalues and Eigenvectors
$A \v =\left( \lambda I\right)\v$
$\lambda I = \left(\begin{array}{ccc} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda \\ \end{array}\right) $
Eigenvalues and Eigenvectors
$A \v =\left( \lambda I\right)\v$
$\Ra \,A \v -\left( \lambda I\right) \v=\mathbf 0$
$\Ra \,\left(A - \lambda I\right) \v=\mathbf 0$
Eigenvalues and Eigenvectors
$\underbrace{\left(A - \lambda I\right)}{} \v=\mathbf 0$
This matrix looks like $\qquad\qquad\qquad $
$ \left(\begin{array}{ccc} 3-\lambda & -1 & 2 \\ 2 & 5-\lambda & 4 \\ 1 & 3 & 5-\lambda \\ \end{array}\right) $$\qquad\qquad \qquad$
Eigenvalues and Eigenvectors
$\left(A - \lambda I\right) \v=\mathbf 0$
We want a nonzero vector $\v$ satisfying this equation.
For this, recall that
$ \text{det}\left(A - \lambda I\right) =0 $
Eigenvalues and Eigenvectors
$\left(A - \lambda I\right) \v=\mathbf 0$
$ \text{det}\left(A - \lambda I\right) =0 $
Example
Consider the matrix $A = \left(\begin{matrix} 3 & 1 \\ 0 & 2 \end{matrix}\right). $
First, to compute the eigenvalues $\lambda,$ we set the matrix
$A - \lambda I $ $ = \left(\begin{matrix} 3- \lambda & 1 \\ 0 & 2 -\lambda \end{matrix}\right). $
Then we compute the determinant
$ \text{det} \left(\begin{matrix} 3- \lambda & 1 \\ 0 & 2 -\lambda \end{matrix}\right) $ $ = \left(3- \lambda \right)\left(2- \lambda \right) $ $ = 0. $
Thus the eigenvalues are $\lambda =2$ and $\lambda = 3.$
Example
Consider the matrix $A = \left(\begin{matrix} 3 & 1 \\ 0 & 2 \end{matrix}\right). $
Thus the eigenvalues are $\lambda =2$ and $\lambda = 3.$
To figure out an eigenvector corresponging to the eigenvalue $\lambda =2,$ we plug in this value to the matrix
$ \left(\begin{matrix} 3- \lambda & 1 \\ 0 & 2 -\lambda \end{matrix}\right) $ $= \left(\begin{matrix} 3- 2 & 1 \\ 0 & 2 -2 \end{matrix}\right). $
Then we use our equation $\,\left(A-\lambda I\right)\v = \mathbf 0\,$ to obtain
$ \left(\begin{matrix} 3- 2 & 1 \\ 0 & 2 -2 \end{matrix}\right) \left(\begin{matrix} x \\ y \end{matrix}\right)= \left(\begin{matrix} 0 \\ 0 \end{matrix}\right). $
Example
Consider the matrix $A = \left(\begin{matrix} 3 & 1 \\ 0 & 2 \end{matrix}\right). $
$ \left(A-\lambda I\right)\v = \mathbf 0 \,\Ra\, \left(\begin{matrix} 3- 2 & 1 \\ 0 & 2 -2 \end{matrix}\right) \left(\begin{matrix} x \\ y \end{matrix}\right)= \left(\begin{matrix} 0 \\ 0 \end{matrix}\right) $
$ \; \; \Ra\, \left(\begin{matrix} 1 & 1 \\ 0 & 0 \end{matrix}\right) \left(\begin{matrix} x \\ y \end{matrix}\right)= \left(\begin{matrix} 0 \\ 0 \end{matrix}\right) $
$\Ra \left\{ \begin{array}{ccccc} x & +& y & = & 0\\ 0 x &+& 0 y & = & 0\\ \end{array} \right. $ $\;\;\Ra\;\; x = -y. $
Example
Consider the matrix $A = \left(\begin{matrix} 3 & 1 \\ 0 & 2 \end{matrix}\right). $
$\Ra \left\{ \begin{array}{ccccc} x & +& y & = & 0\\ 0 x &+& 0 y & = & 0\\ \end{array} \right. $ $\;\;\Ra\;\; x = -y. $
Thus $\, \v $ $= \left(\begin{matrix} x \\ y \end{matrix}\right) $ $= \left(\begin{matrix} -y \\ y \end{matrix}\right) $ $=y \left(\begin{matrix} -1 \\ 1 \end{matrix}\right),\; $ $ (y \text{ is a scalar}). $
Hence an eigenvector corresponding to $\lambda =2\,$ is $\, \left(\begin{matrix} -1 \\ 1 \end{matrix}\right). $
Example
Consider the matrix $A = \left(\begin{matrix} 3 & 1 \\ 0 & 2 \end{matrix}\right). $
Now to compute an eigenvector corresponging to the eigenvalue $\lambda =3,$ we plug in this value to the matrix
$ \left(\begin{matrix} 3- \lambda & 1 \\ 0 & 2 -\lambda \end{matrix}\right) $ $= \left(\begin{matrix} 3- 3 & 1 \\ 0 & 2 -3 \end{matrix}\right). $
Again we use our equation $\,\left(A-\lambda I\right)\v = \mathbf 0\,$ to obtain
$ \left(\begin{matrix} 3- 3 & 1 \\ 0 & 2 -3 \end{matrix}\right) \left(\begin{matrix} x \\ y \end{matrix}\right)= \left(\begin{matrix} 0 \\ 0 \end{matrix}\right). $
Example
Consider the matrix $A = \left(\begin{matrix} 3 & 1 \\ 0 & 2 \end{matrix}\right). $
$ \left(A-\lambda I\right)\v = \mathbf 0 \,\Ra\, \left(\begin{matrix} 3- 3 & 1 \\ 0 & 2 -3 \end{matrix}\right) \left(\begin{matrix} x \\ y \end{matrix}\right)= \left(\begin{matrix} 0 \\ 0 \end{matrix}\right). $
$ \,\Ra\, \left(\begin{matrix} 0 & 1 \\ 0 & -1 \end{matrix}\right) \left(\begin{matrix} x \\ y \end{matrix}\right)= \left(\begin{matrix} 0 \\ 0 \end{matrix}\right) $
$\Ra \left\{ \begin{array}{ccccc} 0x & +& y & = & 0\\ 0x &-& y & = & 0\\ \end{array} \right. $ $\;\Ra y = 0\, $ & $\,x$ is a free variable.
Example
Consider the matrix $A = \left(\begin{matrix} 3 & 1 \\ 0 & 2 \end{matrix}\right). $
$\Ra \left\{ \begin{array}{ccccc} 0x & +& y & = & 0\\ 0x &-& y & = & 0\\ \end{array} \right. $ $\;\Ra y = 0\, $ & $\,x$ is a free variable.
Thus $\, \v $ $= \left(\begin{matrix} x \\ y \end{matrix}\right) $ $= \left(\begin{matrix} x \\ 0 \end{matrix}\right) $ $=x \left(\begin{matrix} 1 \\ 0 \end{matrix}\right),\; $ $ (x \text{ is a scalar}). $
Hence an eigenvector corresponding to $\lambda =3\,$ is $\, \left(\begin{matrix} 1 \\ 0 \end{matrix}\right). $
Example
Consider the matrix $A = \left(\begin{matrix} 3 & 1 \\ 0 & 2 \end{matrix}\right). $
In summary
|
Problem 5
Find the eigenvalues and eigenvectors of
a) \( \left( \begin{array}{r} \sqrt{2} & 1 \\ 1 & \sqrt{2} \end{array} \right) \)
b) \( \left( \begin{array}{r} 5 & 4 \\ 3 & 1 \end{array} \right) \)
b) \( \left( \begin{array}{r} 1 & 1 \\ 1 & 1 \end{array} \right) \)