Linear Algebra
&
Engineering Mathematics 1

Week 11 - Probability


Probability Mass Functions vs Probability Discrete Functions

When we talk about random variables(RVs) in probability, they come in two types:

  • Discrete: Take on specific, separate values (like 0, 1, 2...).
  • Continuous: Can take on any value within a range (like any real number between 0 and 6).
Probability Mass Functions vs Probability Discrete Functions

For discrete random variables we use a probability mass function (PMF) written as: \[ f_X(x) = Pr(X = x) \]

This means: "What is the probability that the random variable $X$ is exactly equal to the value $x$?"

Example: Tossing a fair die. 🎲 → $Pr(X=4)=\dfrac{1}{6}.$

To find the probability that $X$ lies in a range (like $2 ≤ X ≤ 4$), we add up the individual probabilities: \[ Pr(2\leq X \leq 4) = f_X(2) + f_X(3) + f_X(4). \]


Probability Mass Functions vs Probability Discrete Functions

For continuous random variables, we use a probability density function (PDF), denoted also by $f_X(x).$

Unlike discrete variables, we cannot calculate probabilities at exact points:

For all real numbers $a$: $\;Pr(X = a) = 0.$

Instead, we calculate probabilities over intervals using integration: \[ Pr(a\lt X\lt b) = \int_a^bf_X(x)\,dx \]

This integral represents the area under the curve of the PDF between $a$ and $b,$ which gives the probability that $X$ lies within that range.


Summary: Discrete vs Continuous Random Variables
Random Variable Type Function Name Notation Probability for Range
Discrete PMF (mass) \( f_X(x) \) \( \ds \Pr(X \in A) = \sum_{x \in A} f_X(x) \)
Continuous PDF (density) \( f_X(x) \) \( \ds\Pr(a < X < b) = \int_a^b f_X(x)\,dx \)


Example: Throwing a fair die 🎲

The probability that any of one of the six sides of a fair die 🎲 lands uppermost when thrown is 1/6. This can be represented be represented mathematically as: \[ P(X = x) = \frac{1}{6}, \hspace{0.3 cm} x = 1, 2, \ldots, 6. \]

  • \(X\) represents the random variable describing the side that lands uppermost.
  • \(x\) represents the possible values \(X\) can take.
Cumulative Density Function (CDF)

The cumulative density function (CDF) of a random variable is the probability that the random variable takes a value less than or equal to a specified value, $x$: \[ F(x) = Pr(X \leq x) \]

$X$ 1 2 3 4 5 6
$f_X(x)$ $\dfrac{1}{6}$ $\dfrac{1}{6}$ $\dfrac{1}{6}$ $\dfrac{1}{6}$ $\dfrac{1}{6}$ $\dfrac{1}{6}$
$F(x)$ $\dfrac{1}{6}$ $\dfrac{2}{6}$ $\dfrac{3}{6}$ $\dfrac{4}{6}$ $\dfrac{5}{6}$ $\dfrac{6}{6}$

👆 Throwing a die 🎲


Cumulative Density Function (CDF)

$F(x) = Pr(X \leq x)$

$X$ 1 2 3 4 5 6
🔵 $f(x)$ $\dfrac{1}{6}$ $\dfrac{1}{6}$ $\dfrac{1}{6}$ $\dfrac{1}{6}$ $\dfrac{1}{6}$ $\dfrac{1}{6}$
— $F(x)$ $\dfrac{1}{6}$ $\dfrac{2}{6}$ $\dfrac{3}{6}$ $\dfrac{4}{6}$ $\dfrac{5}{6}$ $\dfrac{6}{6}$

👆 Throwing a die 🎲


Cumulative Density Function (CDF)
The uniform distribution (Discrete & Continuous)
Checkpoint: Problem 1

Let $X$ denote the random variable that measures the sum of the sides that come up when rolling two fair dice 🎲🎲 simultaneously.

  1. Write down the sample space of $X$ (what are possible values of $X$?)
  2. Write down the probability mass function (PMF) of $X,$ in a tabular form.
  3. Use the PMF in part 2 to write down the cumulative distribution function (CDF) of $X$ in a tabular form.

Die 2
Die 1
    1       2       3       4       5       6   
 1  1, 1 1, 2 1, 3 1, 4 1, 5 1, 6
 2  2, 1 2, 2 2, 3 2, 4 2, 5 2, 6
 3  3, 1 3, 2 3, 3 3, 4 3, 5 3, 6
 4  4, 1 4, 2 4, 3 4, 4 4, 5 4, 6
 5  5, 1 5, 2 5, 3 5, 4 5, 5 5, 6
 6  6, 1 6, 2 6, 3 6, 4 6, 5 6, 6

Checkpoint: Problem 1

Let $X$ denote the random variable that measures the sum of the sides that come up when rolling two fair dice 🎲🎲 simultaneously.

  1. Write down the sample space of $X$ (what are possible values of $X$?)
  2. Write down the probability mass function (PMF) of $X,$ in a tabular form.
  3. Use the PMF in part 2 to write down the cumulative distribution function (CDF) of $X$ in a tabular form.









Checkpoint: Problem 2

The continuous random variable $Y$ is uniformly distributed on the interval $(1,2).$

  1. Write down the probability density function (PDF) of $Y.$
  2. Sketch the graph of the pdf of $Y.$
  3. By thinking about the geometry of the PDF, write down a formula for the CDF of $Y$ (you do not have to do integration to work this out). Sketch this CDF.






Checkpoint: Problem 2

The continuous random variable $Y$ is uniformly distributed on the interval $(1,2).$

  1. Write down the probability density function (PDF) of $Y.$
  2. Sketch the graph of the pdf of $Y.$
  3. By thinking about the geometry of the PDF, write down a formula for the CDF of $Y$
    (you do not have to do integration to work this out). Sketch this CDF.









Bayes' Theorem

Suppose we have two events: $A$ and $B.$ The probability of both occurring simultaneously is

1. $P(A \text{ and } B) = P\left(A \,|\, B\right)P(B)$

2. $P(A \text{ and } B) = P\left(B \,|\, A\right)P(A)$

This implies $\,P\left(A \,|\, B\right)P(B) = P\left(B \,|\, A\right)P(A)$

⭐️ $P\left(A \,|\, B\right)= \dfrac{P\left(B \,|\, A\right)P(A)}{P(B)}$ ⭐️



Bayes' Theorem

⭐️ $P\left(A \,|\, B\right)= \dfrac{P\left(B \,|\, A\right)P(A)}{P(B)}$ ⭐️

Since $P(B) =$ $\, P\left(B \,|\, A\right)P(A) $ $\,+$ $\, P\left(B \,|\, A'\right)P(A'),$ then


$P\left(A \,|\, B\right)= \dfrac{P\left(B \,|\, A\right)P(A)}{P\left(B \,|\, A\right)P(A) + P\left(B \,|\, A'\right)P(A')}$


Example 👉 Medical Diagnosis


The Normal Distribution

$ \large f_X(x; \mu, \sigma) =\ds \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2} \left( \frac{x - \mu}{\sigma} \right)^2}, $

$x \in \R,\, \mu \in \R, \sigma > 0,$

The Normal Distribution

$ \large N\left(\mu, \sigma^2\right) =\ds \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2} \left( \frac{x - \mu}{\sigma} \right)^2}$

We write $X\sim N\left(\mu, \sigma^2\right)$:

$X$ is normally distributed with mean $\mu$ and variance $\sigma^2.$

The Normal Distribution

Areas under the Standard Normal Distribution
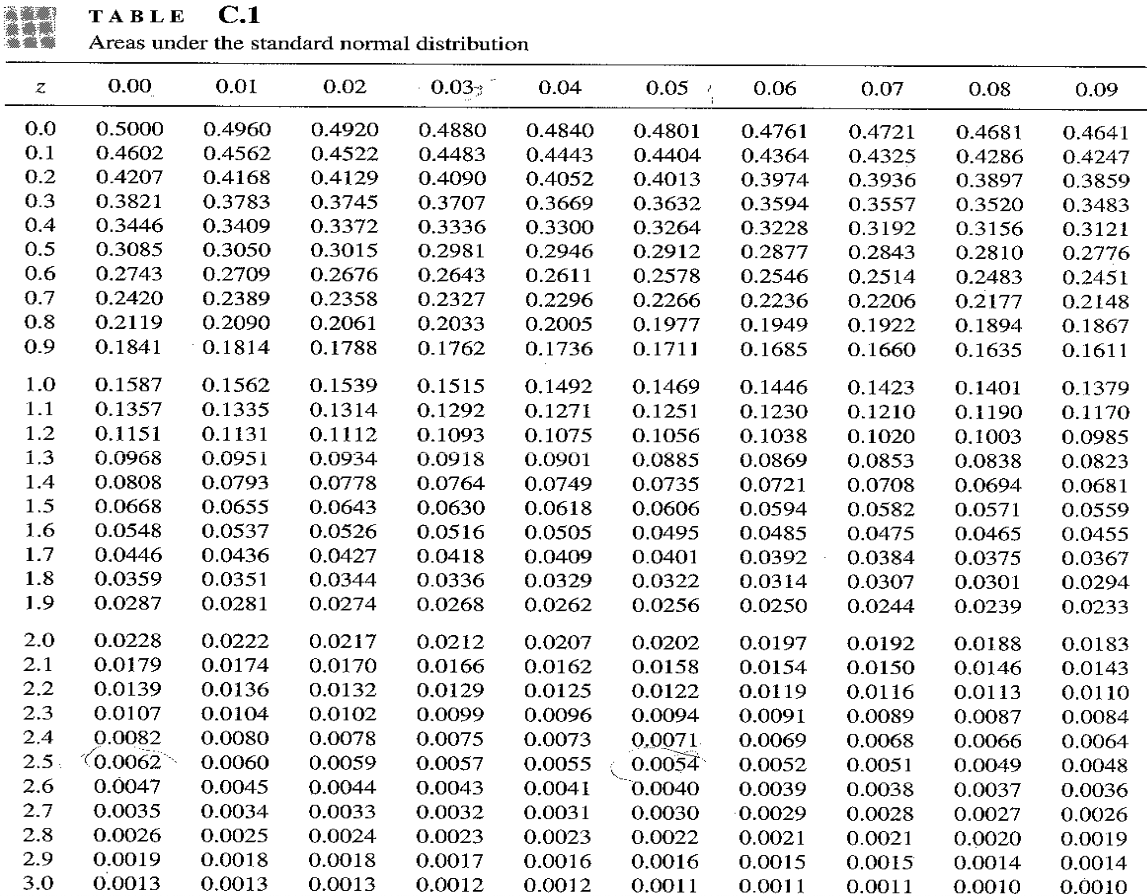
Areas under the Standard Normal Distribution
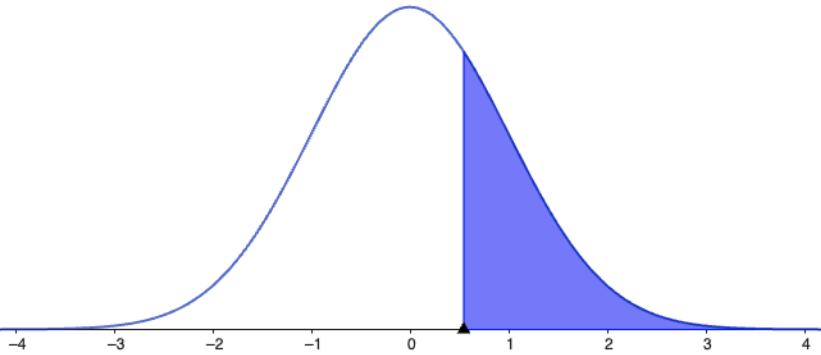
👈 $Z\sim N(0,1)$
$P(Z\gt a)$
Areas under the Standard Normal Distribution

Example 1: $Z \sim N(0,1).$ Find $P(Z\gt 1.52)$


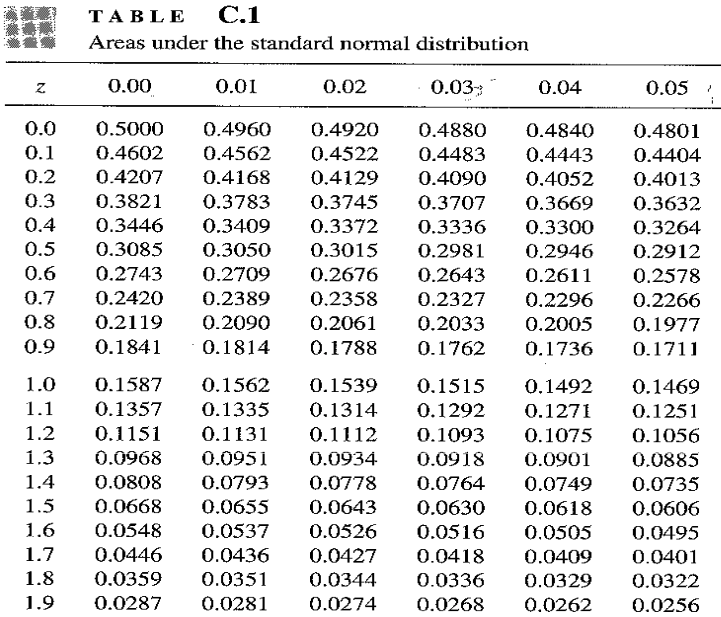
Areas under the Standard Normal Distribution

Example 2: $Z \sim N(0,1).$ Find $P(0 \lt Z \lt 1.52)$


Areas under the Standard Normal Distribution

Exercise 1: Find $P( Z \lt -1.93)\qquad \;\,\,$

Exercise 2: Find $P( -1.52 \lt Z \lt 1.52)$


Example: How to apply the transformation $Z = \frac{x-\mu}{\sigma}$

Many university students do some part-time work to supplement their allowances. In a study on students' wages earned from part-time work, it was found that their hourly wages are normally distributed with mean, $\mu = \$ 16.20$ and standard deviation $\sigma = \$3.$ Find the proportion of students who do part-time work and earn more than $25.00 per hour.








Probability distributions

$P(X=k)$ $=$ $^nC_k $ $p^{\,k}$ $(1-p)^{n-k}$


Probability distributions
Normal distribution: \[ N\left(\mu, \sigma^2\right) =\ds \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2} \left( \frac{x - \mu}{\sigma} \right)^2} \]
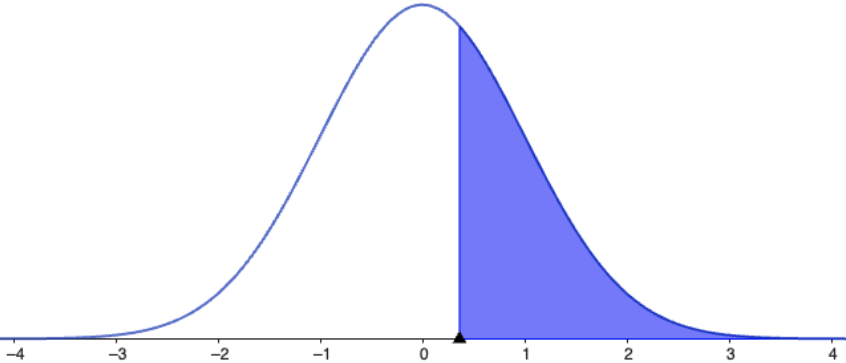
Poisson distribution: \[ P\left(X=k\right) =\ds \frac{e^{-\lambda }\lambda^k}{k!}, \;k = 0, 1, \ldots, \lambda \gt 0 \]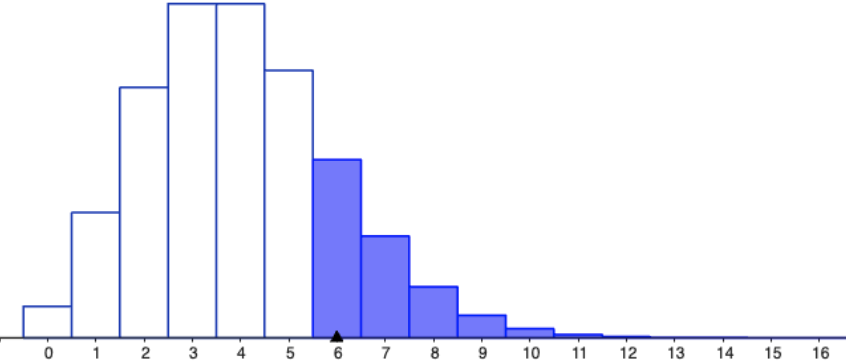
Exponential distribution: \[ f_X(x) =\ds \left\{ \begin{array}{rl} \lambda e^{-\lambda x}, & x\geq 0\\ 0, & \text{otherwise} \end{array} \right. \]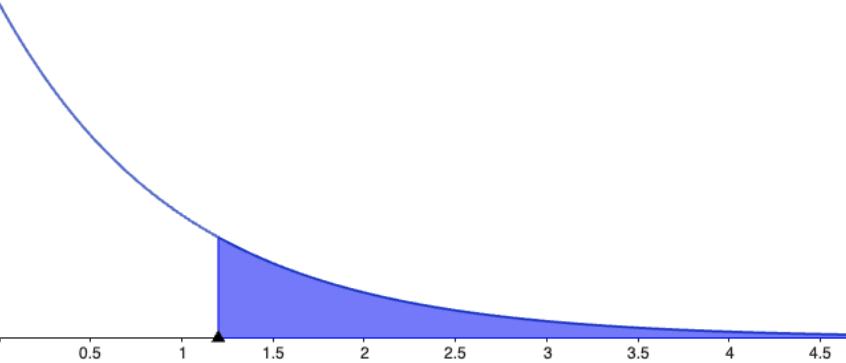
Key properties of the Poisson distribution

\[ P\left(X=k\right) =\ds \frac{e^{-\lambda }\lambda^k}{k!} \]

  • $k$ is the number of occurrences ($k = 0, 1, \ldots$ ).
  • $\lambda $ is a positive parameter ($\lambda \gt 0$) known as the rate of occurrence.
  • $E(X) = \lambda .$
  • If $X_1, X_2,\ldots , X_n$ are independent Poisson random variables with parameters $\lambda_1,\lambda_2,\ldots,\lambda_n,$ respectively, then

    $X =\ds \sum_{k=1}^{n}X_i $ $\ds \sim \text{Poisson}\left(\sum_{k=1}^{n}\lambda\right)$


Probability distributions

Open tool


Checkpoint: Bank Tellers Problem

The manager of a bank branch supervises three tellers. The number of customers each teller can serve in a 10-minute period follows a Poisson distribution, but with different rates: Teller A serves customers at a rate of 2 per 10 minutes, Teller B at a rate of 3 per 10 minutes, and Teller C at a rate of 4 per 10 minutes.

  1. If the tellers serve customers independently of each other, write down the probability distribution of the total number of customers this branch can serve in a 10 minute period when fully staffed.
  2. How many customers would you expect this branch to serve in a 10 minute period if fully staffed?
  3. Calculate the probability that the total number of customers served in a 10 minute period at this branch exceeds 5 people, when fully staffed.


Checkpoint: Bank Tellers Problem
  1. If the tellers serve customers independently of each other, write down the probability distribution of the total number of customers this branch can serve in a 10 minute period when fully staffed.

Let \( X_A \sim \text{Poisson}(2) ,\) \( X_B \sim \text{Poisson}(3),\) and \( X_C \sim \text{Poisson}(4) ,\)

All independent.

The total number of customers served is:

$ X = X_A + X_B + X_C $ $\ds \sim \text{Poisson}(2 + 3 + 4) = \text{Poisson}(9)$



Checkpoint: Bank Tellers Problem
  1. How many customers would you expect this branch to serve in a 10 minute period if fully staffed?

\( X_A \sim \text{Poisson}(2) ,\) \( X_B \sim \text{Poisson}(3),\) \( X_C \sim \text{Poisson}(4) ,\) independent.

The expected value of a Poisson distribution is its rate parameter \( \lambda \). Thus

$ E(X) $ $= 2 + 3 + 4 =9$




Checkpoint: Bank Tellers Problem
  1. Calculate the probability that the total number of customers served in a 10 minute period at this branch exceeds 5 people, when fully staffed.

We want to compute \( P(X > 5) \) where \( X \sim \text{Poisson}(9) .\)
Use the complement rule:

$ \quad P(X > 5) = 1 - P(X \leq 5) $ $= 1 - \ds \sum_{k=0}^{5}P\left(X=k\right) $

$ \qquad \qquad = 1 - \left[ \ds \frac{e^{-9}9^{0}}{0!} + \frac{e^{-9}9^{1}}{1!} + \frac{e^{-9}9^{2}}{2!} + \frac{e^{-9}9^{3}}{3!} + \frac{e^{-9}9^{4}}{4!} + \frac{e^{-9}9^{5}}{5!}\right] $



Key properties of the Exponential distribution

\[ f_{X}(x)=\ds \left\{ \begin{array}{rl} \lambda e^{-\lambda x}, & x\geq 0\\ 0, & \text{otherwise} \end{array} \right. \]

  • We write $X\sim Exp(\lambda).$
  • The CDF of $X\sim Exp(\lambda)$ is

    $\quad P(X\lt x)=$ $\ds F_X(x) =\ds \left\{ \begin{array}{rl} 1-e^{-\lambda x}, & x\geq 0\\ 0, & \text{otherwise} \end{array} \right.$

  • $E(X) = \dfrac{1}{\lambda} $ and $\text{Var}(X) = \dfrac{1}{\lambda^2}.$
  • If $X\sim Exp(\lambda),$ then \[ \qquad \qquad P\left(X\gt s+t \,|\, X\gt t\right) = P\left( X\gt s\right). \]