Linear Algebra
&
Engineering Mathematics 1

Week 12 - Functions


Elementary functions

Polynomials

Trigonometric functions

Exponentials & Logarithms


🚀 Motion of Objects/Particles Affected by Gravity

$y(x) = \ds \frac{g}{2u^2} x^2+\frac{v}{u}x$


☕️ Law of Cooling & 🧫 Population Growth
\(T(t)=\left(T_0-T_m\right) e^{-kt} + T_m\) $\ds P(t) = \frac{\theta P_0 e^{rt}}{\theta-P_0+P_0e^{rt}}$


🔬 Hooke's Law (Spring Force)

Force needed to stretch a spring:

\[ F(x) = kx \]

  • Linear function
  • \( x \): displacement in meters
  • \( k \): spring constant (stiffness)

Used in physics, biomechanics, engineering.



🔬 Hooke's Law (Spring Force)

The undamped spring

Use mouse to drag mass and release.

$x(t) = A \sin \left(\omega t \right)$

Source code


🔬 Hooke's Law (Spring Force)

The undamped spring


🔬 Hooke's Law (Spring Force)

Damped spring. Use mouse to drag mass and release.

Source code


📊 Linear Regression

Predicting height from age: Suppose we collect data from children aged 2 to 13 and record their heights.


📊 Linear Regression

Predicting height from age:

The data points suggest a linear trend:

\[ h(a) = 6.58a + 70.36 \]

📈 Linear Regression

Predicting height from age:

The data points suggest a linear trend:

\[ h(a) = 6.58a + 70.36 \]

  • \( a \): age in years
  • \( h(a) \): predicted height in cm
  • Slope \( 6.58 \): average growth per year

This line is the line of best fit — found using linear regression.


Polynomial Regression

$y = a_0 + a_1x + a_2x^2 + \cdots + a_nx^n + \epsilon$

We look for a least squares polynomial function of best fit.


💊 Medicine in the Body

Drug concentration decreases over time:

\[ C(t) = C_0 e^{-kt} \]

  • Exponential decay
  • \( C_0 \): initial concentration
  • \( k \): decay constant

Models how the body metabolizes medicine.



💊 Medicine in the Body

\[ C(t) = 100 e^{-0.3t} \]

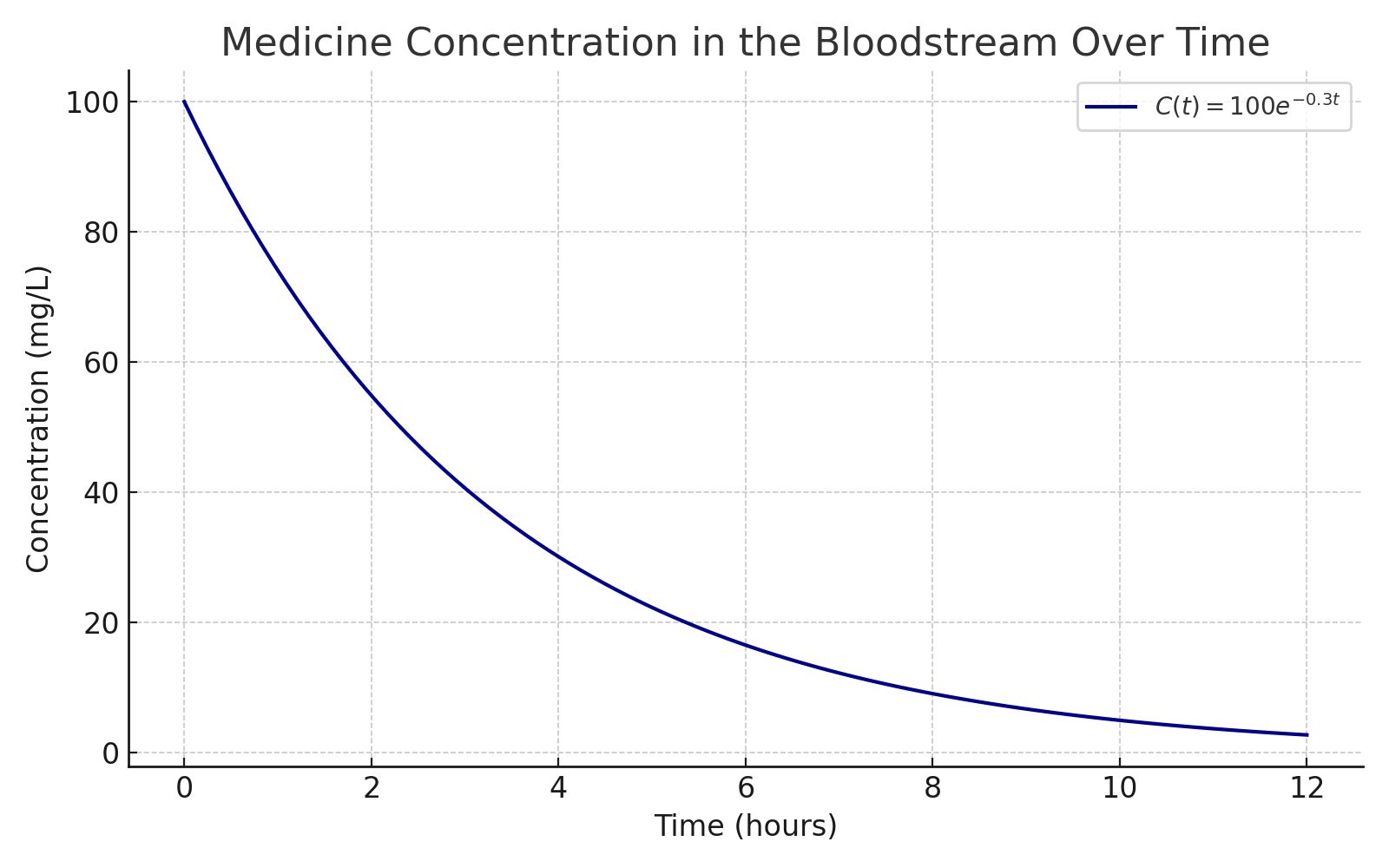
This is a classic example of exponential decay, useful in pharmacology for understanding how a drug's concentration diminishes after administration.


Trigonometric functions: Waveform Analysis

Author: Lucas V. Barbosa


Trigonometric functions & Complex Numbers 🤯










Discrete Fourier Transform


Trigonometric functions: Procedural Landscape Generation

\[ f(\mathbf{x}) = \sum_{i=0}^{N-1} A_i \cdot \left[\cos\left(2\pi \, \mathbf{k}_i \cdot \mathbf{x} + \phi_i\right) + \sin\left(2\pi \, \mathbf{k}_i \cdot \mathbf{x} + \theta_i\right)\right] \]

   Combined with Linear Algebra
to visualise the 3D surface! 🤯

Open live demo


Computer Graphics & Art

Desmos 3D graph   -   Iñigo Quilez


Computer Graphics & Art


$f(x) = \sqrt{6^2-x^2}$

$g(x) = 2 + 2 \sin(\text{floor}(x-t) 4321)$

$h_k(x) = \dfrac{-5}{k}+\dfrac{2}{5}, $

$\qquad k=0,1,\ldots, 10$

Graphtoy


Elementary functions
Function Expression
Polynomials \(a_nx^n + a_{n-1}x^{n-1}+\cdots a_1 x + a_0\)
Trigonometric \(\sin x, \cos x, \tan x\)
Inverse Trigonometric \(\arcsin x, \arccos x, \arctan x\)
Exponentials \(e^x,\; b^x\)
Logarithms \(\ln x, \;\log_b(x)\)
Hyperbolic \(\sinh x, \cosh x, \tanh x\)
Inverse Hyperbolic \(\text{arcsinh}\, x, \text{arccosh}\, x, \text{arctanh}\, x\)
Absolute value \(|x|\)
Square root \(\sqrt{x}\)


Found Functions

Photos by Nikki Graziano


Time in a Bottle by Jim Croce


Problem 1

For each equation below, determine whether it represents a function. If it does, identify its domain and range.

  1. \( y^3 = x \)
  2. \( y^4 = x \)
  3. \( y = \tan(\alpha) \)
  4. \( y = 4 \)







Problem 1

For each equation below, determine whether it represents a function. If it does, identify its domain and range.

  1. \( y^3 = x \)
  2. \( y^4 = x \)
  3. \( y = \tan(\alpha) \)
  4. \( y = 4 \)







Problem 1

For each equation below, determine whether it represents a function. If it does, identify its domain and range.

  1. \( y^3 = x \)
  2. \( y^4 = x \)









Problem 1

For each equation below, determine whether it represents a function. If it does, identify its domain and range.

  1. \( y = \tan(\alpha) \)
  2. \( y = 4 \)









Problem 2

A weight is oscillating on the spring. The equilibrium position of the object is $x=2m,$ the amplitude of the oscillations is $0.2 m.$ If we look at the object's oscillations, it will be in the equilibrium position at times $t=0s,$ $t=2s,$ $t=4s,$ $t=6s,\ldots.$ What is the equation describing position of the object in time?









Problem 3

Sketch the following functions:

  1. The number of radioactive nuclei versus time, assuming the initial number is 100,000 on day 0 and it halves every 6 days on average.
     
  2. The velocity of a falling ball, assuming it starts from rest and its velocity increases by 9.81 m/s every second (i.e., constant acceleration due to gravity).
     
  3. \( f(x) = \left\{\begin{array}{rl}-1, & x\lt 0 \\ x^2, & 0\leq x\lt 2\\ x, & 2 \leq x \end{array}\right. \)

GeoGebra plot   -   Desmos plot




Problem 3

Sketch the following functions:

  1. The number of radioactive nuclei versus time, assuming the initial number is 100,000 on day 0 and it halves every 6 days on average.
     
  2. The velocity of a falling ball, assuming it starts from rest and its velocity increases by 9.81 m/s every second (i.e., constant acceleration due to gravity).
     
  3. \( f(x) = \left\{\begin{array}{rl}-1, & x\lt 0 \\ x^2, & 0\leq x\lt 2\\ x, & 2 \leq x \end{array}\right. \)



Problem 3

Sketch the following functions:

  1. The number of radioactive nuclei versus time, assuming the initial number is 100,000 on day 0 and it halves every 6 days on average.
     









Problem 3

Sketch the following functions:

  1. The velocity of a falling ball, assuming it starts from rest and its velocity increases by 9.81 m/s every second (i.e., constant acceleration due to gravity).
     








Problem 3

Sketch the following functions:

  1. \( f(x) = \left\{\begin{array}{rl}-1, & x\lt 0 \\ x^2, & 0\leq x\lt 2\\ x, & 2 \leq x \end{array}\right. \)
     







Problem 4

Sketch the following functions:

  1. $f_1(x)= 2\sin(3x)$
  2. $f_2(x)= 4\cos(2x)-1$
  3. \(f_3(x) = 2e^{-3x}\)
  4. $f_4(x) = x^2-x-2 $
  5. $f_5(x) = (x+1)x(x-1)$





Problem 5

Find the inverse of each of the following functions:

  1. $f_1(x)= 2\sin(3x)$
  2. $f_2(x)= \dfrac{x}{x+1}$
  3. \(f_3(x) = 2e^{-3x}\)
  4. $f_4(x) = x^2-x-2 $

Are the inverse functions actually functions (i.e., do they pass the vertical line test)? Can you easily plot the inverse functions?

Exploring Inverse functions tool





Problem 5

Find the inverse of each of the following functions:

  1. $f_1(x)= 2\sin(3x)$
  2. $f_2(x)= \dfrac{x}{x+1}$
  3. \(f_3(x) = 2e^{-3x}\)
  4. $f_4(x) = x^2-x-2 $

Are the inverse functions actually functions (i.e., do they pass the vertical line test)? Can you easily plot the inverse functions?





Problem 5

Find the inverse of each of the following functions:

  1. $f_1(x)= 2\sin(3x)$

Are the inverse functions actually functions (i.e., do they pass the vertical line test)? Can you easily plot the inverse functions?









Problem 5

Find the inverse of each of the following functions:

  1. $f_2(x)= \dfrac{x}{x+1}$

Are the inverse functions actually functions (i.e., do they pass the vertical line test)? Can you easily plot the inverse functions?









Problem 5

Find the inverse of each of the following functions:

  1. \(f_3(x) = 2e^{-3x}\)
  2. $f_4(x) = x^2-x-2 $

Are the inverse functions actually functions (i.e., do they pass the vertical line test)? Can you easily plot the inverse functions?









Problem 6

Consider the following functions: $f(x) = 2x,$ $g(x) = x^2+1 $ and $h(x)= e^{\sqrt{x}}.$ Find

  1. $f\bigg(g\big( h\left(x\right) \big)\bigg)$
  2. $g\bigg(h\big(f(x) \big)\bigg)$
  3. $h\bigg(f\big( g(x) \big)\bigg)$







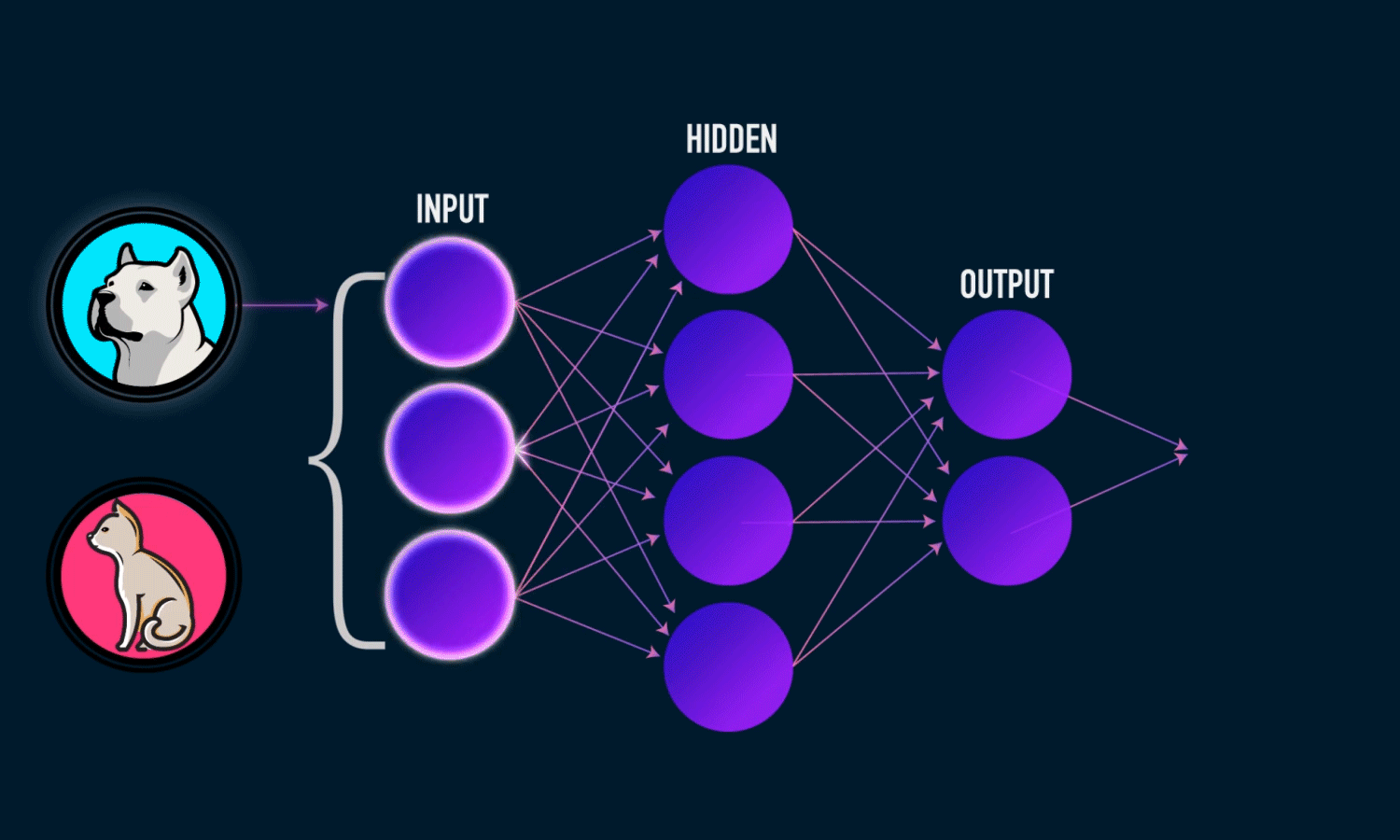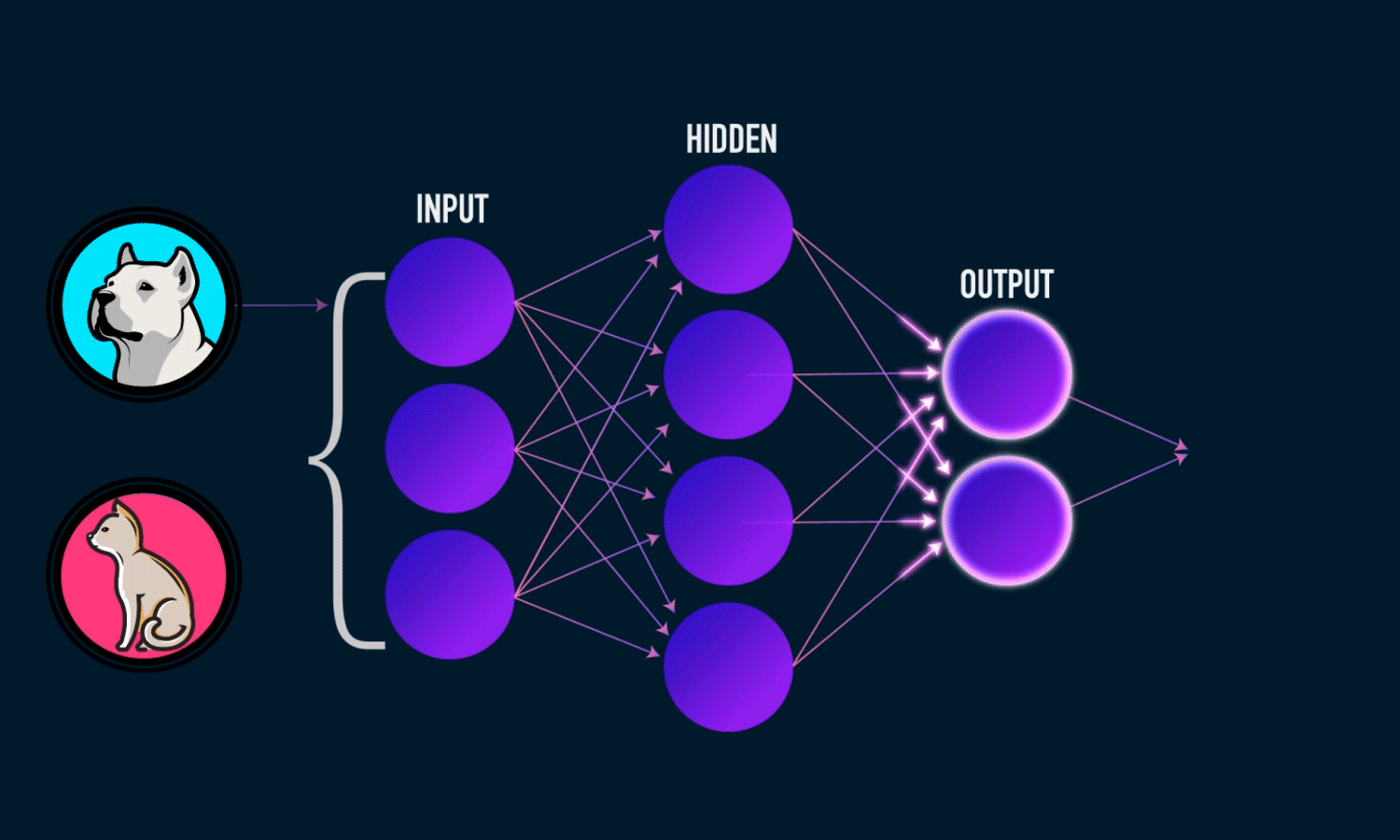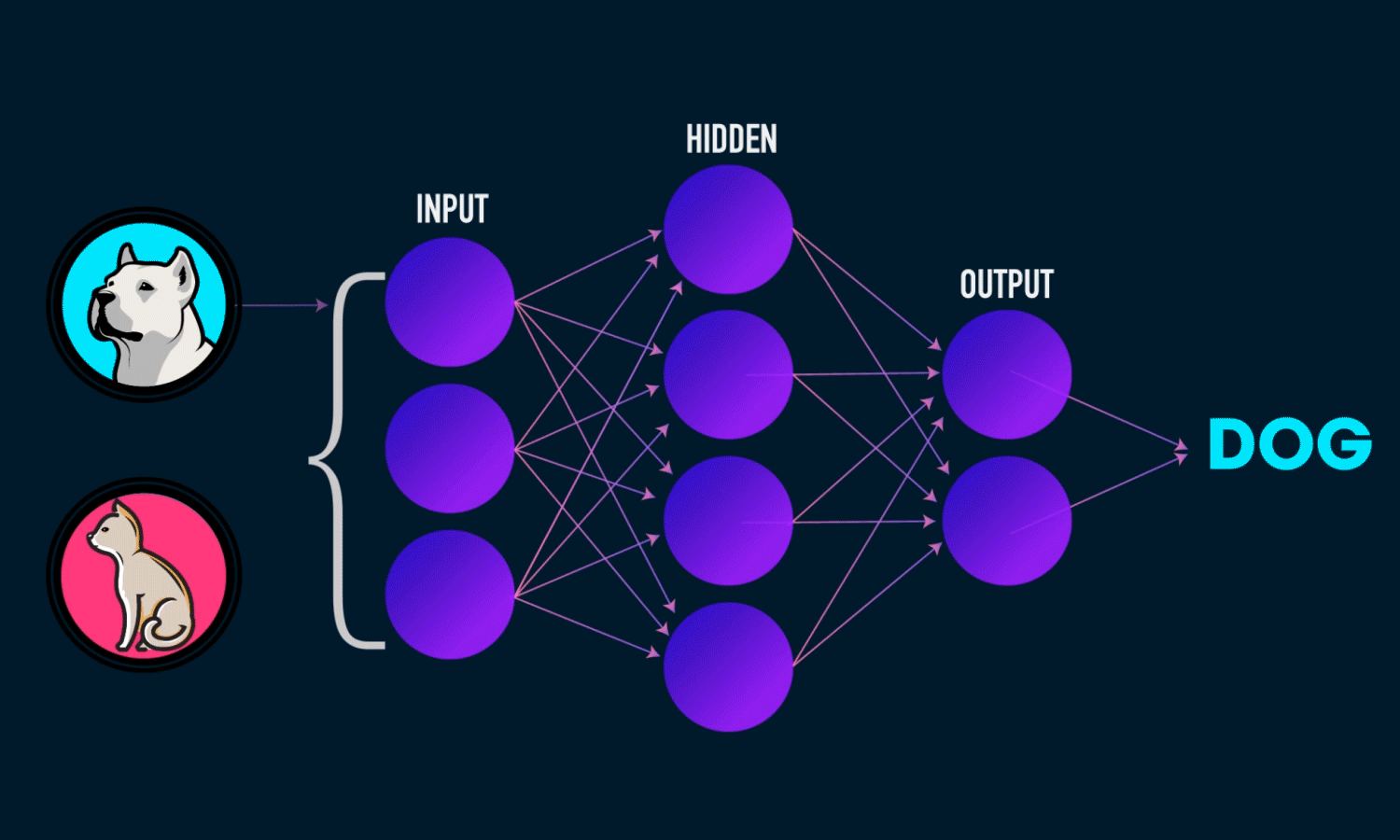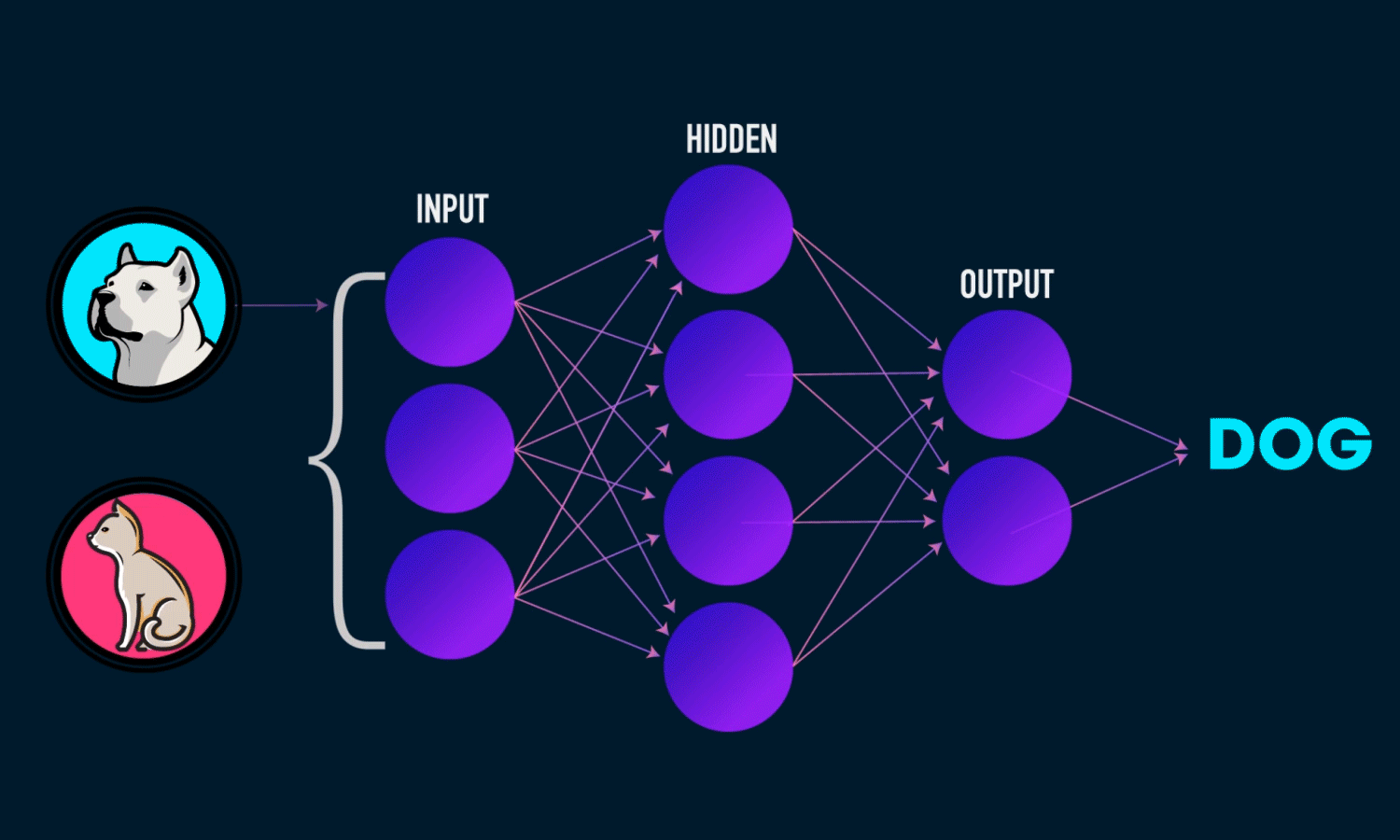
Neural Networks

Source