
Quantitative Reasoning
1015SCG
Lecture 2
Units of measurement
Units
|
|
Source: A Brief History of the Metric System by Carmen J. Giunta (2023).
Units
|
|
||||||||||||||||||||||||||
Source: A Brief History of the Metric System by Carmen J. Giunta (2023).
Units: Other physical quantities
Any other physical quantities can be written as some combination of these base units, and are sometimes are given their own name.
- $\text{velocity}= \dfrac{\text{distance}}{\text{time}}$ $=\dfrac{\text{m}}{\text{s}}$
- $\text{acceleration}= \dfrac{\text{velocity}}{\text{time}}$ $=\dfrac{\text{m}/\text{s}}{\text{s}}$ $=\dfrac{\text{m}}{\text{s}^2}$
- $\text{force}= \text{mass}\times \text{acceleration}$ $=\text{kg}\times \dfrac{\text{m}}{\text{s}^2}$ $=\text{N}$ $\;\; $(Newton)
- $\text{pressure}= \dfrac{\text{force}}{\text{area}}$ $= \dfrac{\text{N}}{\text{m}^2}$ $= \dfrac{\text{kg}\times \dfrac{\text{m}}{\text{s}^2}}{\text{m}^2}$ $= \dfrac{\text{kg}}{\text{m}\times\text{s}^2}$ $= \text{Pa}$ $\;\;$(Pascal)
- $\text{energy}= \text{mass}\times \text{velocity}^2$ $= \text{kg} \times \dfrac{\text{m}^2}{\text{s}^2}$ $= \dfrac{\text{kg}\times \text{m}^2}{\text{s}^2}$ $= \text{J}$ $\;\;$(Joule)
Other sets of units
There are a number of non-SI units accepted for use alongside SI units, e.g.:
- Angle in degrees, minutes and seconds (e.g. latitude and longitude).
- Area in hectares.
- Volumes in litres.
- Time in minutes, hours, days, years.
- Temperature in degrees Celsius.
Other sets of units
People in the U.S. uses customary units in daily life (related to the British Imperial system), e.g.:
-
Lengths in inches, feet, yards, miles and area in
acres. - Mass in pounds.
- Temperatures in degrees Fahrenheit (F)
- Ounces (oz) for mass and fluid ounces (fl oz) for volume.
Metric and Imperial system
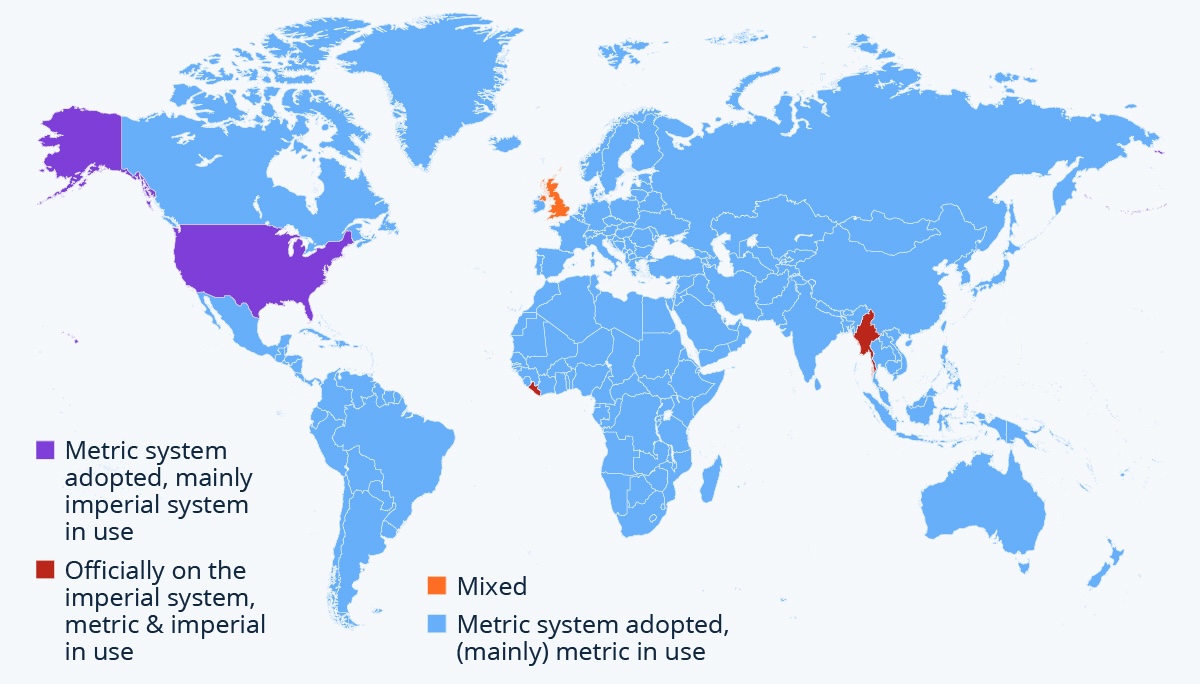
Image source: Statista: Metric or Imperial? (2019)
📝 Practice: Examples
1. The length of the stick is measured to be 70 cm. But you want to
communicate with your American friend. How many inches it is?
Hint: 1 inch = 2.54 cm.
2. The pasture is a rectangle with dimensions of 500 m by 2 km. How
many hectares it is?
Hint: 1 ha = 100 m × 100 m.
3. An Olympic swimming pool has dimensions 50 m × 25 m × 2 m. How
many liters of water it can fit?
Hint: 1 L = 10 cm × 10 cm × 10 cm.
4. The conversion from Fahrenheit to Celsius degrees is
\(^{\circ}\text{C} = \dfrac{5}{9}\left(^{\circ}\text{F}-32\right).\)
Find
(a) \(\,0^\circ\text{F}\) in \(^\circ \text{C},\qquad\)
(b) \(\, 100^\circ\text{F} \) in \(^\circ\text{C},\qquad\)
(c) \(\, -40^\circ\text{C} \) in \(^\circ\text{F}\)
📝 Practice: Examples
1. The length of the stick is measured to be 70 cm. But you want to
communicate with your American friend. How many inches it is?
Hint: 1 inch = 2.54 cm.
We need a conversion factor! Since we know that 1 inch = 2.54 cm, then
\( \dfrac{\text{1 inch}}{\text{2.54 cm}} = 1 \) 👈 This is a conversion factor!
Thus we have
\(70 \text{ cm}\) \(=70 \text{ cm} \times 1\) \(=70 \text{ cm} \times \dfrac{\text{1 inch}}{\text{2.54 cm}} \) \(= \dfrac{70}{2.54} \text{ inch}\) \(= 27.56 \text{ inch}\)
📝 Practice: Examples
2. The pasture is a rectangle with dimensions of 500 m by 2 km.
How many hectares is it?
Hint: 1 ha = 100 m × 100 m.
Let's start by finding the area in square metres.
First, we knot that \(2\,\text{km} = 2000\,\text{m}\)
Area = \(500 \text{ m} × 2\,000 \text{ m} \) \(= 1\,000\,000 \text{ m}^2\)
Now use the conversion factor from $\text{m}^2$ → $\text{ha}$:
\(1 \text{ ha} = 100 \text{ m} × 100 \text{ m} \)
\(= 10\,000 \text{ m}^2\)
\(\dfrac{1 \text{ ha}}{10\,000 \text{ m}^2} = 1\) 👈 Conversion factor
\(1\,000\,000 \text{ m}^2 × \dfrac{1 \text{ ha}}{10\,000 \text{ m}^2} \) \(= 100 \text{ ha}\)
📝 Practice: Examples
3. An Olympic swimming pool has dimensions 50 m × 25 m × 2 m.
How many litres of water can it fit?
Hint: 1 L = 10 cm × 10 cm × 10 cm
= 1 000 cm³
= 0.001 m³
First, find the volume in cubic metres.
Volume = \(50\text{ m} × 25\text{ m} × 2 \text{ m}\) \(= 2\,500 \text{ m}^3\)
Now use the conversion between cubic metres and litres:
\(1 \text{ m}^3 = 1\,000 \text{ L}\)
\(\dfrac{1\,000 \text{ L}}{1 \text{ m}^3} = 1\) 👈 Conversion factor
\(2\,500 \text{ m}^3 × \dfrac{1\,000 \text{ L}}{1 \text{ m}^3} \) \(= 2\,500\,000 \text{ L}\)
📝 Practice: Examples
4. The conversion from Fahrenheit to Celsius degrees is
\(^{\circ}\text{C} = \dfrac{5}{9}\left(^{\circ}\text{F}-32\right).\)
Find:
(a) \(0^\circ\text{F}\) in
\(^{\circ}\text{C},\qquad\)
(b) \(100^\circ\text{F}\) in \(^{\circ}\text{C},\qquad\)
(c) \(-40^\circ\text{C}\) in \(^{\circ}\text{F}\)
💫(a) For \(0^\circ\text{F}\) in \(^{\circ}\text{C}\): \(\; ^{\circ}\text{C} = \dfrac{5}{9}(0 - 32) \) \(= \dfrac{5}{9}(-32)\) \(= -17.78^{\circ}\text{C}\)
💫(b) For \(100^{\circ}\text{F}\): \(\;^{\circ}\text{C} = \dfrac{5}{9}(100 - 32)\) \( = \dfrac{5}{9}(68)\) \(= 37.78^{\circ}\text{C}\)
💫(c) Now convert \(-40^{\circ}\text{C}\) to \(^{\circ}\text{F}\), use the inverse formula: \(^{\circ}\text{F} = \dfrac{9}{5}{}^{\circ}\text{C} + 32\)
Thus \(\; ^{\circ}\text{F} = \dfrac{9}{5}(-40) + 32\) \( = -72 + 32 \) \( = -40^{\circ}\text{F}\)
So, at \(-40^{\circ}\), Celsius and Fahrenheit are equal! ❄️
📝 More practice 😃
- Cheetahs can reach speeds up to 120 km/h.
- How fast is it in m/s?
- What about feet/quarter-hour? (1 foot $\approx$ 30 cm)
- I can paint a wall with the speed of 0.2 $\dfrac{\text{m}^2}{\text{min}}$.
- How long will it take me to paint a 5 m $\times$ 3 m wall?
📝 More practice 😃
- Cheetahs can reach speeds up to 120 km/h.
- How fast is it in m/s?
- What about feet/quarter-hour? (1 foot ≈ 30 cm)
👉 \(120 \text{ km/h} = 120{,}000 \text{ m}/3{,}600 \text{ s} = 33.3 \text{ m/s}\)
👉 \(120 \text{ km/h} = 120{,}000 \text{ m/h} = 400{,}000 \text{ ft/h}\) ⇒ \( 100{,}000 \text{ ft}/ \text{quarted-hour}\)
- I can paint a wall with the speed of 0.2 \(\dfrac{\text{m}^2}{\text{min}}\).
- How long will it take me to paint a 5 m × 3 m wall?
👉 Wall area = \(5\text{ m} \times 3\text{ m} = 15 \text{ m}^2\). Then Time = \(\dfrac{15 \text{ m}^2 }{0.2\frac{\text{m}^2}{\text{min}}} = 75 \text{ min} = 1\text{ h }15\text{ min}\)
Why getting it right is important...

The Gimli Glider was an Air Canada Boeing 767 that ran out of fuel mid-flight in 1983 due to a metric conversion error—the fuel was loaded in pounds instead of kilograms. The pilots glided the plane safely to an emergency landing at a former airbase in Gimli, Manitoba, with no fatalities.
⚠️ Other Famous Conversion Errors
Mars Climate Orbiter (1999): Lost because of a mismatch between
imperial and metric units (pound-seconds vs newton-seconds). See
Mars
climate orbiter

|
Space Mountain, Tokyo Disneyland (2003): Roller coaster axle failed after
parts were made using inch instead of millimeter specifications. See
Unit Mixups

|
Final remarks about the SI
|
|
||||||||||||||||||||||||||
Source: A Brief History of the Metric System by Carmen J. Giunta (2023).
Final remarks about the SI
|
|
||||||||||||||||||||||||||
Source: A Brief History of the Metric System by Carmen J. Giunta (2023).
Scientific Notation, Orders of Magnitude

Image source: visualcapitalist.com
The decimal system
The decimal system
\(= \mathbf 7\times 10 ^3 \) \(+\,\mathbf 5\times 10 ^2 \) \(+\,\mathbf 9\times 10 ^1 \) \(+\,\mathbf 4\times 10 ^0 \)
\(\qquad+\,\mathbf 1\times 10 ^{-1} \) \(+\,\mathbf 6\times 10 ^{-2} \) \(+\,\mathbf 3\times 10 ^{-3} \)
|
|
Really small thingsRadius of a helium atom: $0.000\,000\,000\,031 \text{ m}$ $= 3.1 \times 10^{-11} \text{ m}$ Size of a helium nucleus (alpha particle): $0.000\,000\,000\,000\,000\,002 \text{ m}$ $= 2 \times 10^{-18} \text{ m}$ Mass of a helium atom: $0.000\,000\,000\,000\,000\,000\,000\,000\,006\,64 \text{ kg}$ $= 6.64 \times 10^{-27} \text{ kg}$ |
|
|
Really big thingsGalactic orbit of our sun: $230\,000\,000 \text{ years}$ $=2.3 \times 10^{8} \text{ years}$ The size (diameter) of our galaxy: $950\,000\,000\,000\,000\,000\,000 \text{ m}$ $ = 9.5 \times 10^{20}\text{ m}$ Total mass of stars in the universe: $200\,000\,000\,000\,000\,000\,000$ ✨ $\times$ $2\,000\,000 \,000\,000\,000\,000\,000\,000\,000\,000 \text{ kg}$ $ =\left(2\times 10^{20} \times 2 \times 10^{30} \text{ kg}\right)$ $=4\times 10^{50} \text{ kg}$ |
Normilised Scientific Notation
$ \pm a \times 10 ^{n}$
- $a$ - is called significand, with $\,1\leq a\lt 10$
- $n$ - is the exponent (integer number)
Normilised Scientific Notation
$ \pm a \times 10 ^{n}$
|
|
Writing numbers in normalised scientific notation
- Determine how many places you need to move the decimal point to get a significand at least 1 but less than $10.$
-
Determine the exponent:
- If you move the decimal point to the left, the exponent is positive.
- If you move the decimal point to the right, the exponent is negative.
- Write the number in the form $a\times 10^{n}.$
|
Example 1: $142.14$ $142.14 = 1.4214 \times 10^{2}$ |
Example 2: $0.0312$ $0.0312 = 3.12 \times 10^{-2}$ |
✅ Normalised form: one non-zero digit before the decimal point.
Writing numbers in normalised scientific notation
💻 Calculator/Computer notation
$142.14 = 1.4214 \times 10^{2}$
$\quad \;\,=1.4214\text{E}2$ 👈
$0.0312 = 3.12 \times 10^{-2}$
$\qquad \;\,\;\,=3.12\text{E}-2$ 👈
📝 Write in scientific notation 😃
1. Height of Q1 Tower: $322.5\ \text{m}$
2. Diameter of the Moon: $3\,474\,800\ \text{m}$
3. Average mass of an E.coli cell (wet): $0.000\,000\,000\,001\ \text{g}$
4. Distance between carbon atoms in diamond: $0.000\,000\,000\,154\,4\ \text{m}$
📝 Write in scientific notation 😃
1. Height of Q1 Tower: $322.5\ \text{m}$
$$\textbf{Ans. } 3.225 \times 10^{2}\ \text{m}$$
2. Diameter of the Moon: $3\,474\,800\ \text{m}$
$$\textbf{Ans. } 3.4748 \times 10^{6}\ \text{m}$$
3. Average mass of an E.coli cell (wet): $0.000\,000\,000\,001\ \text{g}$
$$\textbf{Ans. } 1 \times 10^{-12}\ \text{g}$$
4. Distance between carbon atoms in diamond: $0.000\,000\,000\,154\,4\ \text{m}$
$$\textbf{Ans. } 1.544 \times 10^{-10}\ \text{m}$$
SI Metric PrefixesOpen: Full SI Metric Prefixes |
|
Powers of Ten
Example using SI Metric Prefixes
| p | n | µ | m | c | d | da | h | k | M | G |
| $10^{-12}$ | $10^{-9}$ | $10^{-6}$ | $10^{-3}$ | $10^{-2}$ | $10^{-1}$ | $10^{1}$ | $10^{2}$ | $10^{3}$ | $10^{6}$ | $10^{9}$ |
|
The distance between carbon atoms in diamond is $\quad 0.000\,000\,000\,154\,4\ \text{m}$ First, convert to normalized scientific notation $\quad 0.000\,000\,000\,154\,4\ \text{m} $ $= 1.544 \times 10^{-10}\ \text{m}\;$ Not in the SI Metric Prefixes‼️ 👆 But we can write as: $\, 0.1544 \times 10^{-9}\ \text{m} $ $= 0.1544 \, \text{nm} $ ✅ The carbon-carbon distance in diamond is $0.1544 $ nm $\left(154.4\times 10^{-12}\right)$ 👉 or also $154.4 $ pm |
|
Example using SI Metric Prefixes
|
The distance between carbon atoms in diamond is $\quad 0.000\,000\,000\,154\,4\ \text{m}$ First, convert to normalized scientific notation $\quad 0.000\,000\,000\,154\,4\ \text{m} $ $= 1.544 \times 10^{-10}\ \text{m}\;$ If we want to use normalized scientific notation, we can write this in Ångströms (a unit of length). We just need to use the conversion factor: 1 Å = $10^{-10}$ m $\quad 1.544 \times 10^{-10}\ \text{m} $ $= 1.544\ \text{Å}$ ✅ The carbon-carbon distance in diamond is $1.544$ Å |

|
📝 Write using SI Metric Prefixes😃
| p | n | µ | m | cm | d | da | h | k | M | G |
| $10^{-12}$ | $10^{-9}$ | $10^{-6}$ | $10^{-3}$ | $10^{-2}$ | $10^{-1}$ | $10^{1}$ | $10^{2}$ | $10^{3}$ | $10^{6}$ | $10^{9}$ |
1. Age of a dinosaur fossil: $70\,000\,000\ \text{years}=$ _____ Myears
2. Height of Q1 Tower: $322.5\ \text{m}=$ _____ hm = _____ km
3. Diameter of the Moon: $3\,474\,800\ \text{m}=$ ________Mm
4. Average mass of an E.coli cell (wet): $0.000000000001\ \text{g}=$ _____ pg
📝 Write using SI Metric Prefixes 😃
| p | n | µ | m | cm | d | da | h | k | M | G |
| $10^{-12}$ | $10^{-9}$ | $10^{-6}$ | $10^{-3}$ | $10^{-2}$ | $10^{-1}$ | $10^{1}$ | $10^{2}$ | $10^{3}$ | $10^{6}$ | $10^{9}$ |
1. Age of a dinosaur fossil: $70\,000\,000\ \text{years}=$ _____ Myears
$\quad 7 \times 10 ^{7} \text{ years}$ $ = 70 \times 10^6 \text{ years}$ $ = 70 \text{ Myears}$
2. Height of Q1 Tower: $322.5\ \text{m}=$ $3. 225 \text{ hm}$ $= 0.3225 \text{ km}$
$\quad 3.225 \times 10^{2} \text{ m}$ $ = 0.3225 \times 10^{3} \text{ m}$
3. Diameter of the Moon: $3\,474\,800\ \text{m} = 3.4748\ \text{Mm}$
4. Average mass of an E.coli cell (wet): $0.000000000001\ \text{g} = 1\ \text{pg}$
Orders of magnitude — From trillion to trillionth
| Common name | SI prefix (symbol) | Decimal | Power of ten | Order of magnitude |
|---|---|---|---|---|
| Trillion | tera (T) | 1 000 000 000 000 | 1012 | +12 |
| Billion | giga (G) | 1 000 000 000 | 109 | +9 |
| Million | mega (M) | 1 000 000 | 106 | +6 |
| Thousand | kilo (k) | 1 000 | 103 | +3 |
| One | (none) | 1 | 100 | 0 |
| Tenth | deci (d) | 0.1 | 10−1 | −1 |
| Hundredth | centi (c) | 0.01 | 10−2 | −2 |
| Thousandth | milli (m) | 0.001 | 10−3 | −3 |
| Millionth | micro (µ) | 0.000 001 | 10−6 | −6 |
| Billionth | nano (n) | 0.000 000 001 | 10−9 | −9 |
| Trillionth | pico (p) | 0.000 000 000 001 | 10−12 | −12 |
Orders of magnitude
When values vary across a broad scale, it is helpful to think in terms of the exponent $m$, which we call an order of magnitude — $\log_{10}(10^m)$
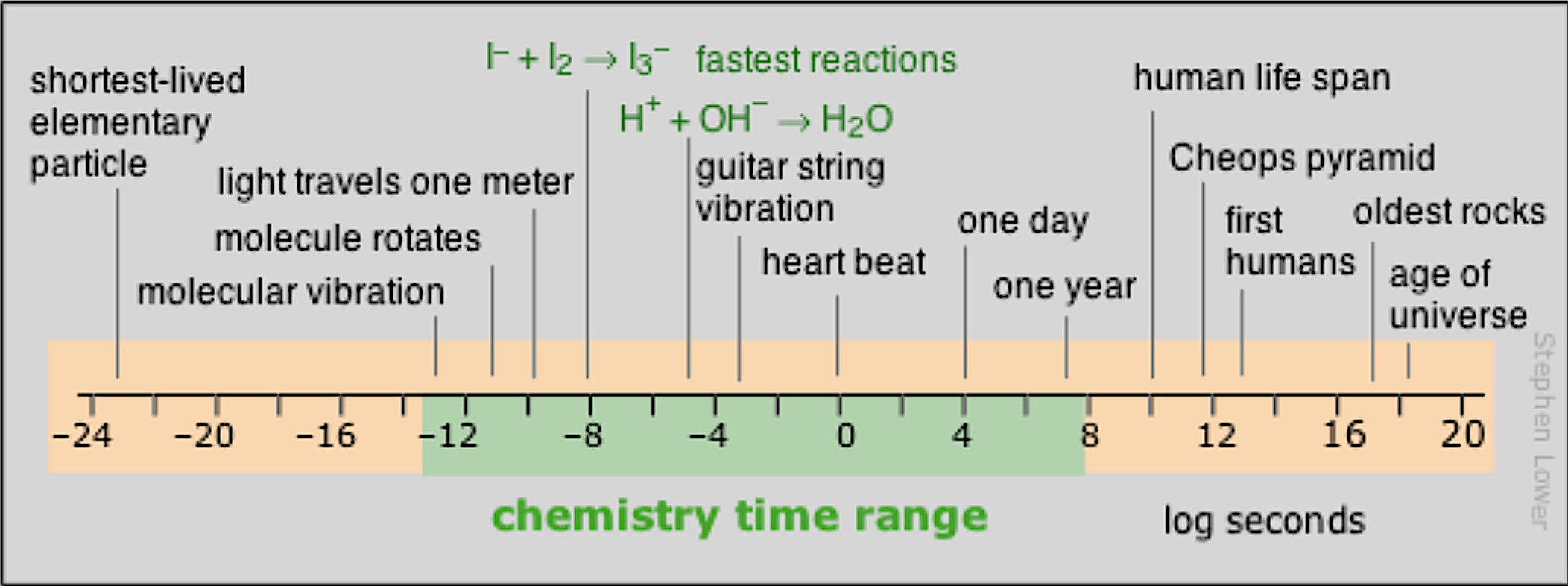
Image source: Chem 1 Virtual Textbook by Stephen Lower
Recap
|
|
Scientific notation or SI Prefixes to convey very small or very large quantities.
👉 Scientific notation ⇔ SI prefixes |
All together now!

🧩 Polya’s Problem-Solving Heuristics
- Understand the problem — Identify what is known, what is unknown, and the conditions.
- Devise a plan — Look for connections to similar problems, use patterns, draw diagrams, simplify, or work backwards.
- Carry out the plan — Execute the strategy carefully, checking each step.
- Look back — Verify results, reflect on the method, and consider generalizations.
Source: How To Solve It, by George Polya, 2nd ed., Princeton University Press, 1957.
📝 Converting between units & relations using units
- What is the height of the Q1 Tower (322.5 m) in microns? $(1\text{ micron} = 1 \,\mu \text{m})$
- What is the age of the universe (1.38 × 10¹⁰ years) in minutes?
-
What is the speed of light (3 × 10⁸ m/s) in AU/hour?
AU is known as the Astronomical Unit, the average distance between Sun and Earth. 1 AU = $150$ billion meters (billion = $10^9$).
-
If a single Tic Tac contains approximately 2 kilocalories (kcal),
how long would it take to burn off the calories?
(a) If sitting $(65 \text{ kcal}/\text{hour})$ (b) If dancing $(150 \text{ kcal}/\text{hour})$
🏢 Q1 Tower Height
What is the height of the Q1 Tower (322.5 m) in microns? $(1\text{ micron} = 1 \,\mu \text{m})$
$1 \text{ metre} = 1 \,000\, 000 \text{ microns }(\mu \text{m})$
$\dfrac{ 1 \,000\, 000 \,\mu\text{m}}{1 \text{ m}} = 1$ 👈 Conversion factor
$\qquad\qquad 322.5 \text{ m}$ $=322.5 \text{ m} \times \dfrac{ 1 \,000\, 000 \,\mu\text{m}}{1 \text{ m}}$
$\qquad\qquad \qquad \quad =3.225 \times 10^{2} \times 10^{6} \,\mu\text{m}$
$\qquad\qquad \qquad \quad =3.225 \times 10^{8} \,\mu\text{m}$
🌌 Age of the Universe
What is the age of the universe (1.38 × 10¹⁰ years) in minutes?
1 year = 365 days = 365 × (24 hours)
= 365 × 24 × (60 mins) = 525 600 mins
1 year = 525 600 mins 👈 Conversion
1.38 × 10¹⁰ years = (1.38 × 10¹⁰) × 525 600 mins $\qquad \qquad \qquad \quad $
= 1.38 × 10¹⁰ × 5.256 × 10⁵ mins = 7.25328 × 10¹⁵ mins
🤔 What value do you get if you consider 1 year = 365.25 day?
⚡ Speed of Light in AU/hour
What is the speed of light (3 × 10⁸ m/s) in AU/hour?
👉 $ $ 1 AU = 1.5 × 10¹¹ m = 150 billion meters
👉 1 hour = 3 600 seconds$\qquad\qquad $
$3 \times 10^{8}\,\dfrac{\text{m}}{\text{s}}$ $= 3 \times 10^{8}\,\dfrac{\text{m}}{\text{s}} \times 3\,600\,\dfrac{\text{s}}{\text{hour}} $ $= 3 \times 10^{8} \times 3\,600\,\dfrac{\text{m}}{\text{hour}} $
$\qquad = 3 \times 10^{8} \times 3\,600\,\dfrac{\text{m}}{\text{hour}} \times \dfrac{1}{1.5\times 10 ^{11}}\, \dfrac{\text{AU}}{\text{m}} $
$\qquad = 3 \times 10^{8} \times 3\,600 \times \dfrac{1}{1.5\times 10 ^{11}}\, \dfrac{\text{AU}}{\text{hour}} $ $= \dfrac{(3\times 3.6) \times 10^{11}}{1.5\times 10 ^{11}}\, \dfrac{\text{AU}}{\text{hour}} $
$\qquad= \dfrac{3\times 3.6 }{1.5}\, \dfrac{\text{AU}}{\text{hour}} $ $= 7.2\, \dfrac{\text{AU}}{\text{hour}} $
🔥 Burning a Tic Tac
If one Tic Tac ≈ 2 kilocalories (kcal), how long to burn it off?
(a) Sitting: $65\,\dfrac{\text{kcal}}{\text{hour}}$ = Rate of burning calories
👉 $\;\text{Rate} = \dfrac{\text{Energy}}{\text{Time}}$ $\;\Ra\; \text{Time} =\dfrac{\text{Energy}}{\text{Rate}}$
Thus $\,\text{Time} = \dfrac{2 \,\text{kcal}}{65\,\frac{\text{kcal}}{\text{hour}}}$ $=\dfrac{2}{65}\,\text{hours}$ $\approx 0.0308\,\text{hours}$ $=1.85\,\text{minutes}$
(b) Dancing: $150\,\dfrac{\text{kcal}}{\text{hour}}$ → $\text{Time} = 0.0133\,\text{hours} \approx 0.8 \,\text{mins}$
⚛️ Mole & Molar mass
Mole (unit)
The mole (mol) is a unit of measurement, the base unit in the SI for amount of substance, an SI base quantity proportional to the number of elementary entities of a substance.
$1\, \text{mol} = 6.022\,140\,76 \times 10^{23}\, \text{entities}$
Molar mass
The molar mass (M) of a chemical substance (element or compound) is defined as the ratio between the mass (m) and the amount of substance (n, measured in moles) of any sample of the substance:
$\text{M} = \dfrac{\text{mass of the substance}}{\text{number of moles of the substance}}$
⚗️ Description of solutions
|
Concentration of the solution (g/L) $\text{Concentration}=\dfrac{\text{mass of the solute}} {\text{volume of the solution}}$ Molar concentration - morality (mol/L) $\text{Morality}=\dfrac{\text{numbers of moles of solute}} {\text{volume of the solution}}$ |

|
⚗️ Other concentrations
\(\%\text{w/w}\) - weight per weight concentration - how many \(\text{g}\) of the solute there are in \(100 \, \text{g}\) of the solution
$\% \dfrac{\text{w}}{\text{w}}=\dfrac{\text{mass of the solute in g}} {100\,\text{g of the solution}}\times 100 \%$
\(\%\text{w/v}\) - weight per volume concentration - how many \(\text{g}\) of the solute there are in \(100 \, \text{ml}\) of the solution
$\% \dfrac{\text{w}}{\text{v}}=\dfrac{\text{mass of the solute in g}} {100\,\text{ml of the solution}}\times 100 \%$
\(\%\text{v/v}\) - volume per volume concentration - how many ml of the solute are there in \(100 \, \text{ml}\) of the solution
$\% \dfrac{\text{v}}{\text{v}}=\dfrac{\text{mass of the solute in ml}} {100\,\text{ml of the solution}}\times 100 \%$
📝 Extra practice 😀
1. What is the concentration and molar concentration of the 0.444 mol of cobalt chloride $\text{CoCl}_2$ in 0.654 L of solution (129.839 g/mol)?
2.
A patient has a serum (39.0983 g/mol) level of 3 mmol/L.
(a) How many mmol are present in a 50 ml sample?
(b) How many mg are present in a 50 ml sample?
3. A glucose solution contains 10% w/v of glucose in water. How much glucose is in 1L of the solution?
4. What weight of hydrochloric acid is needed to produce 50 g of 30% w/w acid?
📝 Extra practice 😀
1. What is the concentration and molar concentration of the 0.444 mol of cobalt chloride $\text{CoCl}_2$ in 0.654 L of solution (129.839 g/mol)?
💫Ans. Mass concentration = 88.15 g/L; Molar concentration = 0.6790 mol/L.
2.
A patient has a serum (39.0983 g/mol) level of 3 mmol/L.
(a) How many mmol are present in a 50 ml sample?
(b) How many mg are present in a 50 ml sample?
💫Ans. (a) 0.150 mmol. (b) 5.865 mg.
3. A glucose solution contains 10% w/v of glucose in water. How much glucose is in 1L of the solution?
💫Ans. 100 g glucose per 1 L.
4. What weight of hydrochloric acid is needed to produce 50 g of 30% w/w acid?
💫Ans. 15 g HCl (to make 50 g of 30% w/w).
📝 Extra practice - Solutions
1. What is the concentration and molar concentration of the 0.444 mol of cobalt chloride $\text{CoCl}_2$ in 0.654 L of solution (129.839 g/mol)?
- Molar concentration (M): \(C = \dfrac{\text{moles}}{\text{volume (L)}} = \dfrac{0.444\ \text{mol}}{0.654\ \text{L}}\).
- Calculate: \(C = \dfrac{0.444\ \text{mol}}{0.654\ \text{L}}= 0.678899\ \text{mol / L}\). Rounded to four decimals: $0.6790 \,\text{mol / L}$
- Mass of solute: \(m = n \times M = 0.444\ \text{mol} \times 129.839\ \text{g / mol} = 57.6485\ \text{g}.\)
- Mass concentration $(\text{g/L})$: \(\rho = \dfrac{m}{V} = \dfrac{57.6485\ \text{g}}{0.654\ \text{L}} = 88.1476\ \text{g / L}.\) Rounded: \(88.15 \,\text{g / L}\)
Thus, Mass concentration = \(88.15 \,\text{g / L}\); Molar concentration = $0.6790 \,\text{mol / L}$.
📝 Extra practice - Solutions
2.
A patient has a serum (39.0983 g/mol) level of 3 mmol/L.
(a) How many mmol are present in a 50 ml sample?
(b) How many mg are present in a 50 ml sample?
- Convert volume to litres: \(50\ \text{mL} = 0.050\ \text{L}.\)
- (a) Amount in mmol: \(n_{\text{mmol}} = C(\text{mmol / L}) \times V(\text{L}) = 3\ \text{mmol / L}\times 0.050\ \text{L} = 0.150\ \text{mmol}.\)
- (b) Mass in mg: 1 mmol corresponds to \(M\,/ \,1000\) g = \(39.0983\ \text{mg}\).
So \(m(\text{mg}) = 0.150\ \text{mmol} \times 39.0983\ \text{mg / mmol} = 5.864745\ \text{mg}.\)
Rounded: 5.865 mg.
Thus, (a) 0.150 mmol; (b) 5.865 mg.
📝 Extra practice - Solutions
3. A glucose solution contains 10% w/v of glucose in water. How much glucose is in 1L of the solution?
- Definition: 10% w/v means 10 g of solute per 100 mL of solution.
- Scale to 1000 mL (1 L): \( \dfrac{10\ \text{g}}{100\ \text{mL}} \times 1000\ \text{mL} = 100\ \text{g}.\)
Thus, the answer is 100 g glucose per 1 L of solution.
📝 Extra practice - Solutions
4. What weight of hydrochloric acid is needed to produce 50 g of 30% w/w acid?
- 30% w/w means mass fraction of solute = 0.30 (i.e. 30 g HCl per 100 g solution).
- Mass of pure HCl required: \(m_{\text{HCl}} = 0.30 \times 50\ \text{g} = 15\ \text{g}.\)
- To prepare the 50 g solution you would combine 15 g HCl with 35 g solvent (usually water) to give a total mass of 50 g.
Hence, the answer is 15 g HCl (to make 50 g of 30% w/w solution).
That's all for today!
See you in Week 3!