1015SCG - Lecture 6

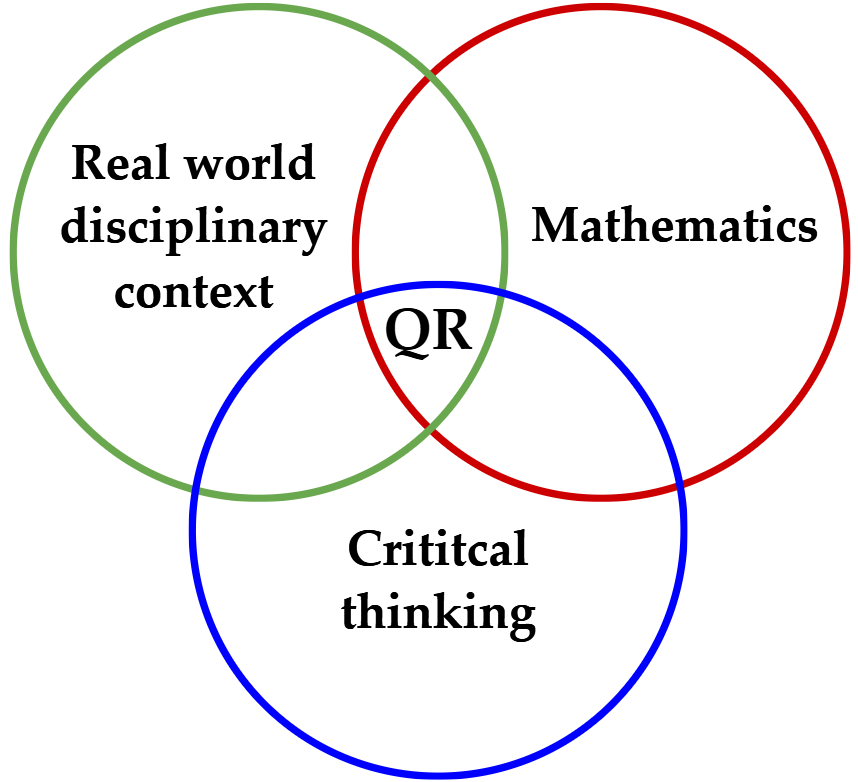
Quantitative Reasoning

1015SCG

Lecture 6

Critical thinking

The art of analyzing and evaluating thinking, with an aim of improving it.
“Thinking about thinking”.
Empowers to understand and critique information.
Provides basis for justifying and evaluating opinions and beliefs.
Allows us to improve and develop our own thinking.
Inspires us to take responsibility for what we believe.
Encourages consistency in our thinking.
Helps us make optimal decisions.

The Scientific Method...

... is a human endeavour and mistakes happen.

Scientific Argumentation

We should be able to defend our ideas and expect that others will do the same.
The opponent challenges (argument) and the proponent defends (counter-argument).
Avoid being aggressive, argumentative, or emotional.
Separate the argument from the person making it.
We easily miss our own mistakes.
The goal is improvement and better results.

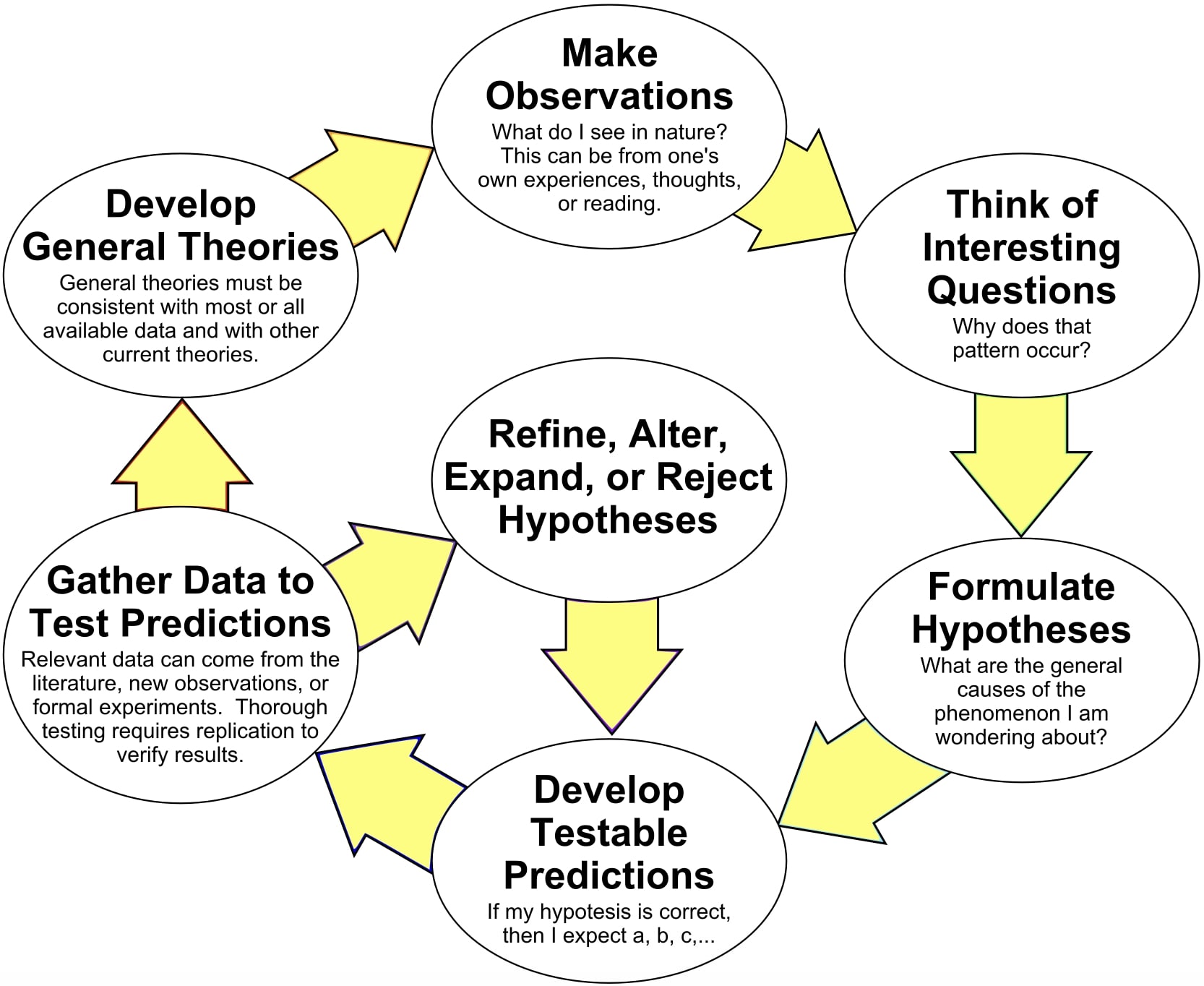
Critical Thinking Skills

Standards (qualities we value)

Clarity
Accuracy
Relevance
Logic

Precision
Significance
Completeness
Fairness

Components (pieces of the process)

Purposes
Questions
Points of view
Information

Inferences
Concepts
Implications
Assumptions

Special elements of critical thinking

Extraordinary claims require extraordinary evidence.
Falsifiability.
Recognizing fallacies and avoiding them.
Balancing induction and deduction.

Problem Posing & Problem Solving

Problem posing

Usual path in teaching maths:
Exposition → Examples → Exercises → Applications.
Real life problems:
A quantitative question with no mathematical context, no data, and no direct means of answering.

Example 🐮

You got a farm, and you want to keep cattle on your farm. The barn you have is a rectangle 20 m by 25 m. The cows will be there to sleep or during bad weather. Otherwise, they have pasture. Which is the best estimate of the number of cows you can fit there?

5
50
500
5 000

👉 Area of barn $ = 20 \text{ m} \times 25 \text{ m}$ $= 500 \text{ m}^2$

Example 🐮

Area of barn $ = 500 \text{ m}^2.$ Estimate how many cows can sleep there.

5 →$\;\dfrac{500 \text{ m}^2}{5 \text{ cows}}$ $= 100{\text{ m}^2}/{ \text{ cow}}$
50 →$\;\dfrac{500 \text{ m}^2}{50 \text{ cows}}$ $= 10{\text{ m}^2}/{ \text{ cow}}$ ✅
500 →$\;\dfrac{500 \text{ m}^2}{500 \text{ cows}}$ $= 1{\text{ m}^2}/{ \text{ cow}}$
5 000 →$\;\dfrac{500 \text{ m}^2}{5000 \text{ cows}}$ $= 0.1{\text{ m}^2}/{ \text{ cow}}$

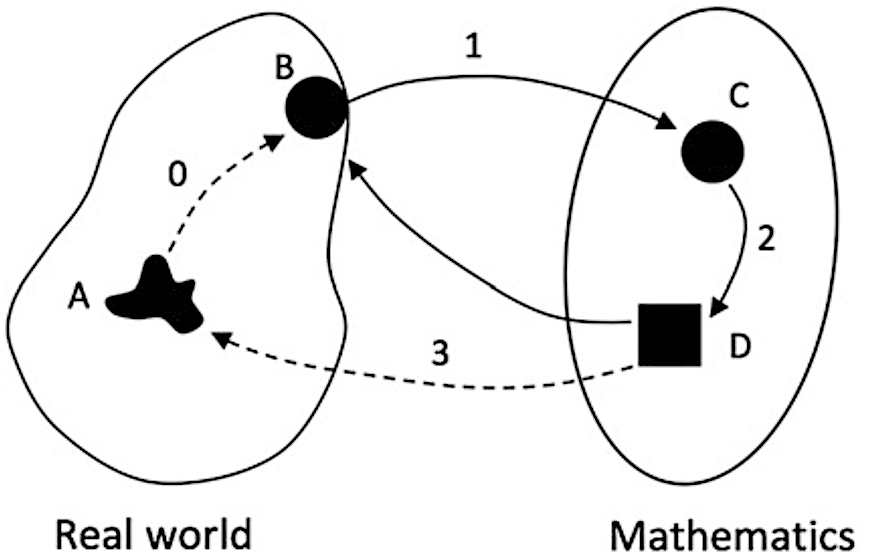
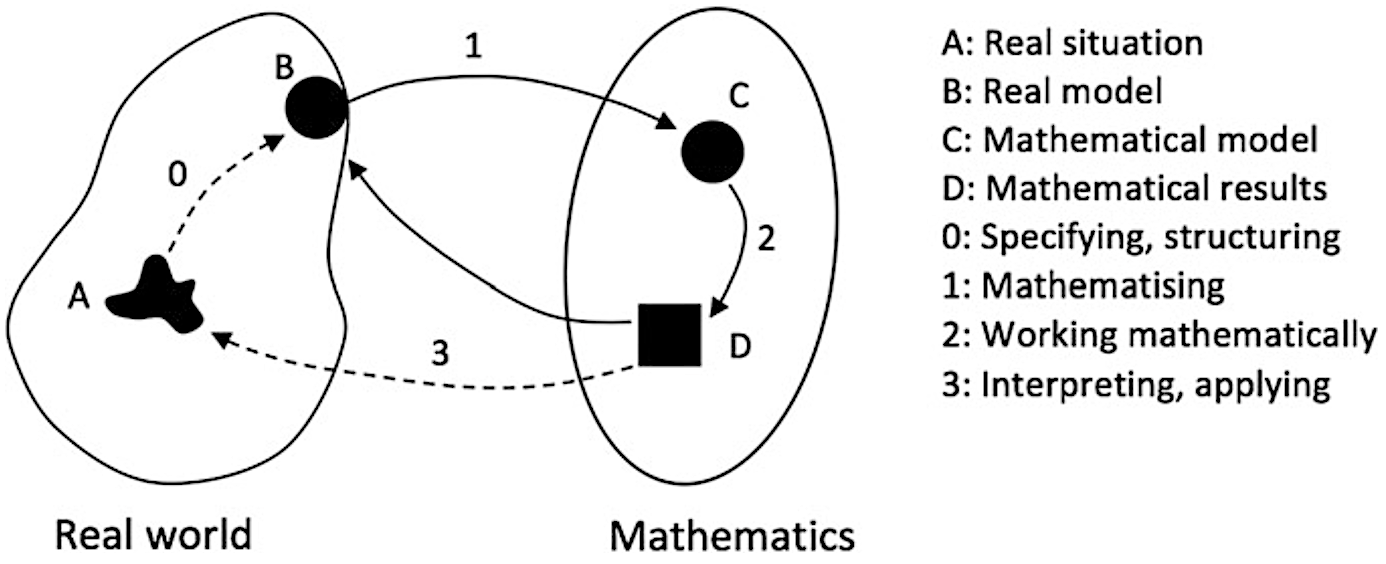
The cycle of mathematical problem posing & problem solving

A: Real situation
— 0. Pick relevant info.

B: Real model
— 1. Mathematize the scenario.

C: Math model
— 2. Do the calculations.

D: Math results
— 3. Revise or return to real situation to choose a reasonable answer.

Blum, W., & Kirsch, A. (1989). The problem of the graphic artist. In W. Blum, J. S. Berry, R. Biehler, I. D. Huntley, G. Kaiser-Meßmer, & L. Profke (Eds.), Applications and modelling in learning and teaching mathematics (pp. 129-135). Chichester: Ellis Horwood.

Recall example about the barn with cows 🐮

A. Real situation: barn with cows.

B. Real model: dimensions, purpose, possible numbers.

C. Math model: compute barn area, estimate space per cow.

D. Math results: area per cow and number of cows per m².

→ Return to real situation to choose a reasonable answer.

Mathematical problem posing & problem solving

Useful skills:

Mathematical content.
Heuristics / strategies / rules of thumb.
Meta-cognition:
- What are you doing?
- Why are you doing it?
- How will it help?
Beliefs and attitudes.

🧩 Mathematical Problem Solving

Polya's four step problem solving method:

Understand the problem
Devise a plan
Carry out the plan
Reflect

Source: How To Solve It, by George Polya, 2nd ed., Princeton University Press, 1957.

🧩 Mathematical Problem Solving

Step 1: Understand the problem.

Do you understand all words?
Can you restate it?
What are you asked to find?
Would a diagram help?
Is the given information enough?

🧩 Mathematical Problem Solving

Step 2: Devise a plan (often hardest).

Relate to similar problems.
Use examples.
Simplify or modify.
Break into smaller parts.
Work backwards.
Use known strategies.

🧩 Mathematical Problem Solving

Step 3: Carry out the plan.

Be patient.
Pay attention to details.
Don't give up too quickly.
Revise if the plan fails.

🧩 Mathematical Problem Solving

Step 4: Reflect.

Can you check the answer?
Could you solve it differently?
Does the result tell you something interesting?
What other problems could be solved with this method?

📝 Practice 😃

☕️ Caffeine

How many 1L bottles can I drink per day?

Recommendation: less than 400 mg caffeine per day.

☕️ Caffeine

1. Understand the problem

Bottle volume: $V_1 = 1\text{ L} = 1000\text{ mL}$
(mL = milliliters)
Example volume: $V_2 = 600\text{ mL}$
Coffee cup vol: $V_3 = 250\text{ mL}$
Coffee in 1cup of coffee: $m_1 = 80\text{ mg}$
(mg = milligrams)
Coffee in $600\text{ mL}$: $m_2 = 1.4 \times m_1 = 112\text{ mg}$
Recommended coffee: $m_3 = 400\text{ mg}$
Number of 1L bottles I can drink = ??
Caffeine per 1L = ??

☕️ Caffeine

2. Devise a plan

Find concentration of caffeine in product $\left[\dfrac{\text{mg}}{\text{mL}}\right]$
$C = \dfrac{\text{Coffee in 600 mL}}{\text{Vol of sol.}}$
Find caffeine per $1\text{ L}$
$ m_4 = C \times 1\text{ L} $
Number of 1L bottles to reach 400 mg:
$ n = \dfrac{\text{Recommended caffeine}}{\text{Caffeine per 1L bottle}} $

☕️ Caffeine

3. Carry out the plan

Find concentration of caffeine in product $\left[\dfrac{\text{mg}}{\text{mL}}\right]$
$C = \dfrac{\text{Coffee in 600 mL}}{\text{Vol of sol.}}$ $= \dfrac{m_2}{V_2}$ $= \dfrac{112\text{ mg}}{600 \text{ mL}}$ $\approx 0.18666\dfrac{\text{ mg}}{\text{ mL}}$
Find caffeine in $1\text{ L}$
$ m_4 = C \times 1\text{ L} $ $=0.18666\dfrac{\text{ mg}}{\text{ mL}} \times 1000\text{ mL}$ $= 1866.6\text{ mg}$
Number of 1L bottles to reach 400 mg:
$ \dfrac{\text{Rec. caffeine}}{\text{Caffeine 1L per bottle}} $ $ = \dfrac{m_3}{m_4} $ $ = \dfrac{400\text{ mg}}{1866.6\frac{\text{mg}}{\text{bottle}}} $ $ \approx 2.14 $

☕️ Caffeine

4. Reflect

So you would need about 2.14 bottles, i.e. at least 3 full 1-L bottles to exceed 400 mg.
We don't need $V_3 = $ cup of coffe volume.

🍕 Pizza party

I want to host a party with 10 people coming. Each person will eat 2/3 of a pizza. My local pizza place has a deal with 2 pizzas for $12. How much will I spend on pizza?

🍕 Pizza Party

1. Understand the Problem

10 people are coming.
Each person eats $ \dfrac{2}{3} $ of a pizza.
Pizzas come in a 2-for-$12 deal.
We will round the total pizza needed up to the nearest even number to use the deal.

🍕 Pizza Party

2. Devise a Plan

Compute total pizza needed: $10 \text{ person} \times \dfrac{2}{3} \dfrac{\text{pizza}}{\text{person}}.\qquad \qquad$
Round this number up to the nearest even integer.
Calculate total cost using the deal (2 pizzas for $12).

🍕 Pizza Party

3. Carry Out the Plan

Total pizza needed:
$10 \text{ person} \times \dfrac{2}{3} \dfrac{\text{pizza}}{\text{person}}$ $ = \dfrac{20}{3} \text{ pizzas}$ $\approx 6.6 \text{ pizzas}\qquad \qquad$
Rounded up to the nearest even number → 8 pizzas.
A deal = 2 pizzas for $\$12$ (that is, 6 dollars per pizza).
Total cost: $6\dfrac{\text{dollars}}{\text{pizza}} \times 8 \text{ pizzas} = \$48$.

🍕 Pizza Party

4. Reflect

Rounding up ensures we buy enough pizza for everyone.
8 pizzas fully uses the 2-for-$12 deal.
Total cost for the party: $48.
You will have extra pizza (good for guests!). 🍕

📝 Extra practice 😃

Car vs tram

Should I drive to Uni or take the tram?

Cans and bottles

I can get 10c for each can and bottle I recycle. But the nearest recycling point is 85 km away. My car burns 6L of gas per 100 km, and the gas costs $2 per liter. How many cans and bottles I need for the trip to pay for itself? What will be the volume of the cans and bottles? How much money I can make?

🤔 Puzzle: A bear leaves point P, walks one mile south, then one mile east, and finally one mile north, returning exactly to point P. What color is the bear?

That's all for today!

See you in Week 7!