Quantitative Reasoning

1015SCG

Lecture 7


Modes of scientific
argumentation


Modes of scientific argumentation

  • Inductive reasoning
  • Deductive reasoning
  • Abductive reasoning





Modes of scientific argumentation

  • Inductive reasoning:
    • rules from observations or experiences;
    • generalisation;
    • poor at truth preserving;
    • can lead to undesirable outcomes

Inductive reasoning: Experiences (A) imply a general rule (B)



🧐 Examples: Inductive reasoning

  • Every time I eat spicy food, I get a stomach-ache.
    Therefore, spicy food causes stomach aches (for me).

  • Every sheep I have seen is white.
    Therefore, all sheep are white.



🧐 Examples: Inductive reasoning

  • If I drop a 🔨 hammer, it falls downwards.
  • If I drop a 🍛 plate, it falls downwards.
  • If I dive into a pool, I fall downwards.
  • Therefore, things fall downwards.
  • I have seen several news reports about teenagers committing crimes.
  • In each case, the offender was a teenager.
  • Therefore, teenagers are criminals. 🤔

Modes of scientific argumentation

  • Deductive reasoning:
    • developing rules based on already known rules;
    • conclusions narrower than underlying rules;
    • easier to correct;
    • starting point — where do we get assumptions?

Deductive reasoning: Assumptions (A) imply logical consequence (B)



🧐 Examples: Deductive reasoning

  • All 🐕 dogs have ears, golden retrievers are dogs,
    therefore they have ears.
  • All mammals have backbones. Humans are mammals. Therefore, humans have backbones.
  • All 🐈 cats can fly. Whiskers is a cat.
    Therefore, Whiskers can fly. 🤔

⭐️ Deductive reasoning preserves truth — but only if the premises are true.


Modes of scientific argumentation

  • Abductive reasoning:
    • is reasoning to the best explanation;
    • It starts from observations or evidence and proposes a plausible hypothesis that would explain them;
    • The conclusion is not guaranteed to be true — it is tentative and revisable.
    • Abductive reasoning contrasts with:
      • Deductive reasoning: guarantees truth if premises are true.
      • Inductive reasoning: generalises from repeated cases.

Abductive reasoning: All our experiences (A) imply the simplest general principles




🧐 Examples: Abductive reasoning

  • While I was reading in bed last night, I started hearing scratching sounds coming from the ceiling. Then, this morning, I noticed there were tiny little droppings on the kitchen floor. I'm pretty sure we have a mice infestation at our house.

  • You walk outside in the morning and see the ground is wet. The sky is clear and there is no rain forecast. You conclude that it probably rained overnight.

Fallacies

  • Fallacy is a false belief
  • Formal/logical fallacy
  • Informal fallacy

Example:

    If it is raining, the ground will be wet.

    The ground is wet.

    Therefore, it must be raining.



Implications

  • A implies B: A ⇒ B
  • If A is true, then B is true as well.
  • Example:

    If it is raining, then the ground is wet.





Implications: Chain rule

We can chain implications:

  • If A ⇒ B and B ⇒ C, then A ⇒ C.
  • Example:

    If it is raining, then the ground is wet.

    If the ground is wet, then Monty does not want to go out.

    Hence, if it is raining, then Monty does not want to go out.



📝 Practice

Consider the following statements:

  • To be President of the US, you must have been born in the US.
  • Anyone born in the US is an American citizen.

Are the following statements true?

  • Any American citizen can become President of the US?
  • Any President of the US is an American citizen?



Sufficient condition

  • A ⇒ B means A is a sufficient condition for B.
  • If A is true, B must be true.
  • But B true does not imply A true.
  • Example:

    If I live in Gold Coast, then I live in Australia.




Necessary condition

  • B ⇒ A means A is a necessary condition for B.
  • B cannot be true unless A is also true.
  • Example:

    If you pass the exam, then you had sat the exam.





Necessary and Sufficient conditions

  • If A is both necessary and sufficient for B: A ⇔ B
  • A ⇔ B can be also written as A iff B (iff short for if and only if)
  • Example:

    A quadrilateral is a square ⇔ it has four equal sides and four right angles.

    A quadrilateral has four equal sides and four right angles ⇔ it is a square.


Necessary and Sufficient conditions

Relationships between statements A and B:

  • A necessary but not sufficient for B.
  • A sufficient but not necessary for B.
  • A equivalent to B (A is both necessary and sufficient for B).
  • A neither necessary nor sufficient for B.




Logical relationships between statements \(A\) and \(B\)

Relationship Symbolic form Notes / equivalent
A necessary
but not sufficient for B 		\( (B \Rightarrow A)\;\land\;\lnot(A \Rightarrow B) \) B implies A,
but A does not imply B.
A sufficient
but not necessary for B 		\( (A \Rightarrow B)\;\land\;\lnot(B \Rightarrow A) \) A implies B,
but B does not imply A.
A equivalent to B \( A \iff B \)
(or \( (A\Rightarrow B)\land(B\Rightarrow A) \)) 		Both implications hold:
A iff B.
A neither necessary
nor sufficient for B 		\( \lnot(A \Rightarrow B)\;\land\;\lnot(B \Rightarrow A) \) Neither implication holds.

Note: The symbol "\(\,\lnot\,\)" means "not".


📝 Practice 😃: Necessary and/or Sufficient

  • a) Watering a plant is a ______ condition for the plant to grow
  • b) Getting $\geq 50\%$ in SUP is a ______ condition for passing
  • c) Winning numbers ticket is a ______ condition for winning lotto
  • d) Getting a degree is a ______ condition for making lots of money



Examples of logical flaws

  1. A ⇒ B then B ⇒ A (invalid)

    If it is raining then the ground is wet.

    Does not imply that: If the ground is wet then it is raining.

  2. A ⇒ B then not A ⇒ not B (invalid)

    If it is raining then the ground is wet.

    Does not imply that: If it is NOT raining then the ground is dry.

  3. Both A and B can not be true. If A is not true, then B must be true.

    If you are not with us, you are against us.


Contrapositives

  • A ⇒ B is equivalent to not B ⇒ not A (\(\lnot B \Ra \lnot A\)).

Example:

Consider the statement: When it is raining, the ground is wet.

Which of the following is logically consistent with this statement?

  • When the ground is wet, it is raining
  • When it isn't raining, the ground isn't wet
  • When the ground isn't wet, it isn't raining.


📝 Putting it all together

  • If you get $\geq$ 50% in your marks throughout the trimester, you pass QR.
  • If you get $\lt$ 45% in your marks throughout the trimester, you fail QR.
  • To qualify for a SUP exam, you must get $\geq $ 45% in your marks throughout the trimester and submit all your assessment.
  • If you get >50% in your SUP for QR, you pass QR.

Are the following statements true?

  • If you passed QR, you got $\geq$ 50% in your marks throughout the trimester.
  • If you don't submit all your assessment, you can't get a SUP.
  • If you failed QR, you got $\lt$ 50% in your marks throughout the trimester.

Informal fallacies

  • Generalization

    It was raining in Hobart when I was there, therefore it always rains in Hobart.

  • Post hoc

    The flowers drooped after the rain, they must not like rain.

  • Straw man

    There is not global warming, because we have a cold winter.

  • Ad hominem

    They don't know anything, they are not epidemiologists.

  • Appeal to authority

    It must be true because Brian Cox said so.

  • Begging the question

    People are buying Samsung phones, therefore Samsung is very popular brand.

  • Black and white

    You are either with us or against us.

Is it TRUE or FALSE? 🤔

This statement is FALSE

If it is true, then it must be false;

if it is false, then it must be true.

Therefore, it cannot be classified as either true or false. 🤯



Is it TRUE or FALSE? 🤔

This statement is FALSE

If it is true, then it must be false;

if it is false, then it must be true.

Therefore, it cannot be classified as either true or false. 🤯

Gödel's Incompleteness Theorem 🎥


Assignment Presentation



Presentation - assignments, exams, homework…

  • How you present your work matters:
    • It affects understanding and marks.
  • In many cases showing working is as important as your final result
    • A wrong final answer doesn't mean your work is useless if your reasoning is clear.
    • It shows how well you understand the ideas involved.
  • You are responsible for presenting your solutions clearly; markers are not required to interpret unclear or incomplete work.

Using software 💻

  • If you use software, say what you used (e. g. Excel, WolframAlpha, Python, etc. ).
  • If you use built-in functions from a specific software, state which ones and on what data.

Example: "I have used STDEV.S function on the number of possums data to find the standard deviation."



Using software 💻

  • If you use built-in functions from a specific software, state which ones and on what data.

If you use a programming language to make some computations, you can comment it in your document and add the full code as an Appendix. 

x = (0:0.25:1);
for j = 1:100
   t = j/25;
   z = sin(pi * x) * cos(2 * pi * t);
   plot(x, z); axis([0,1,-1,1]);
   M(j) = getframe;
end

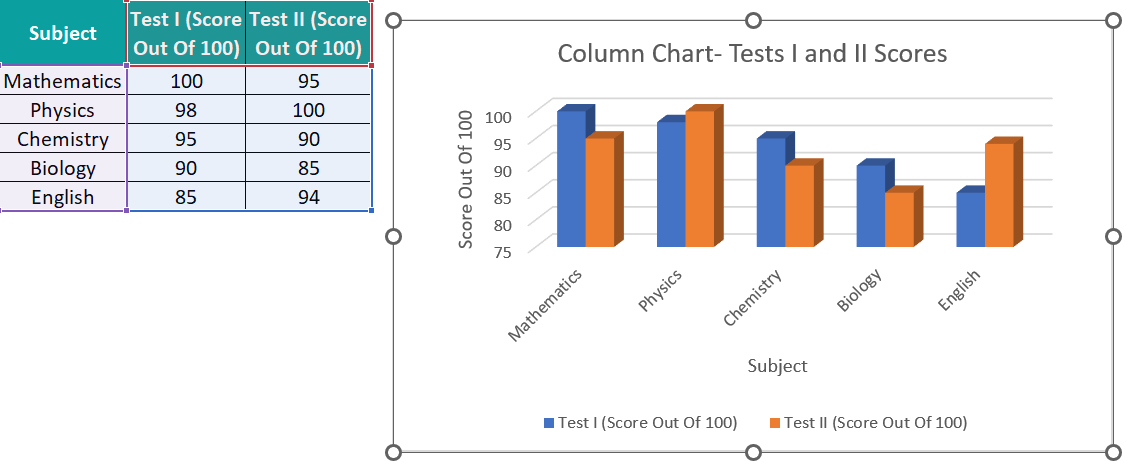
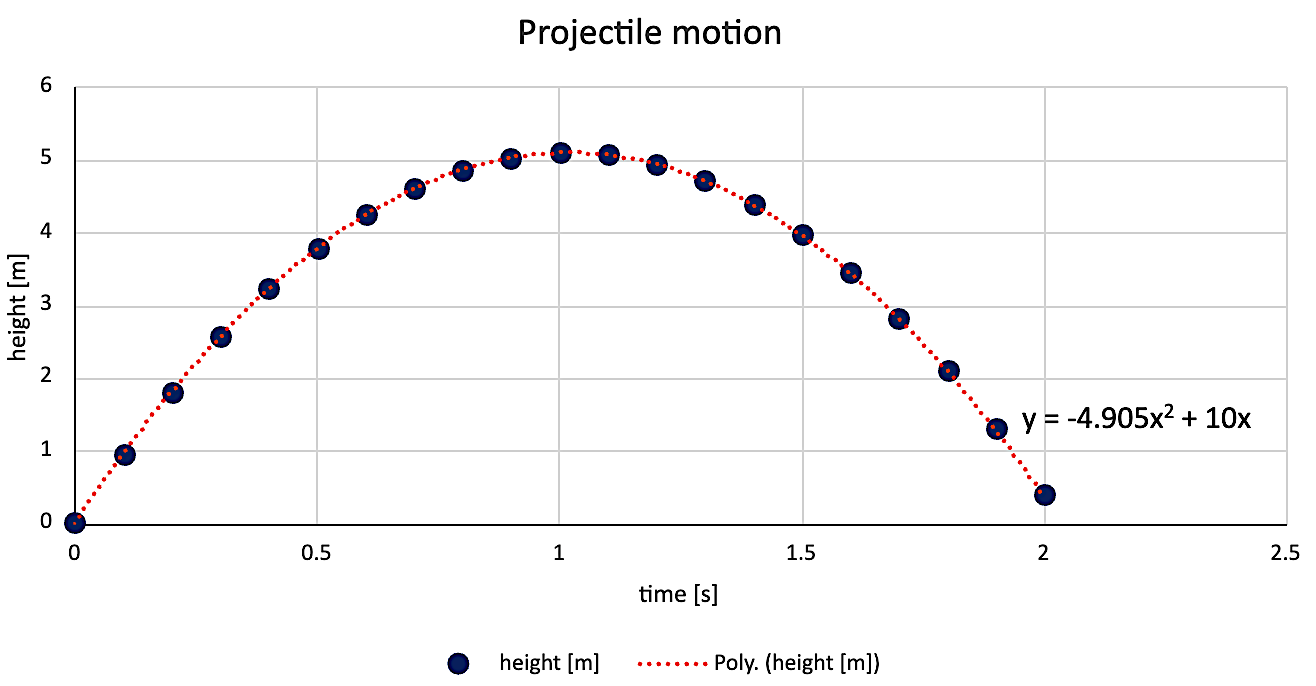
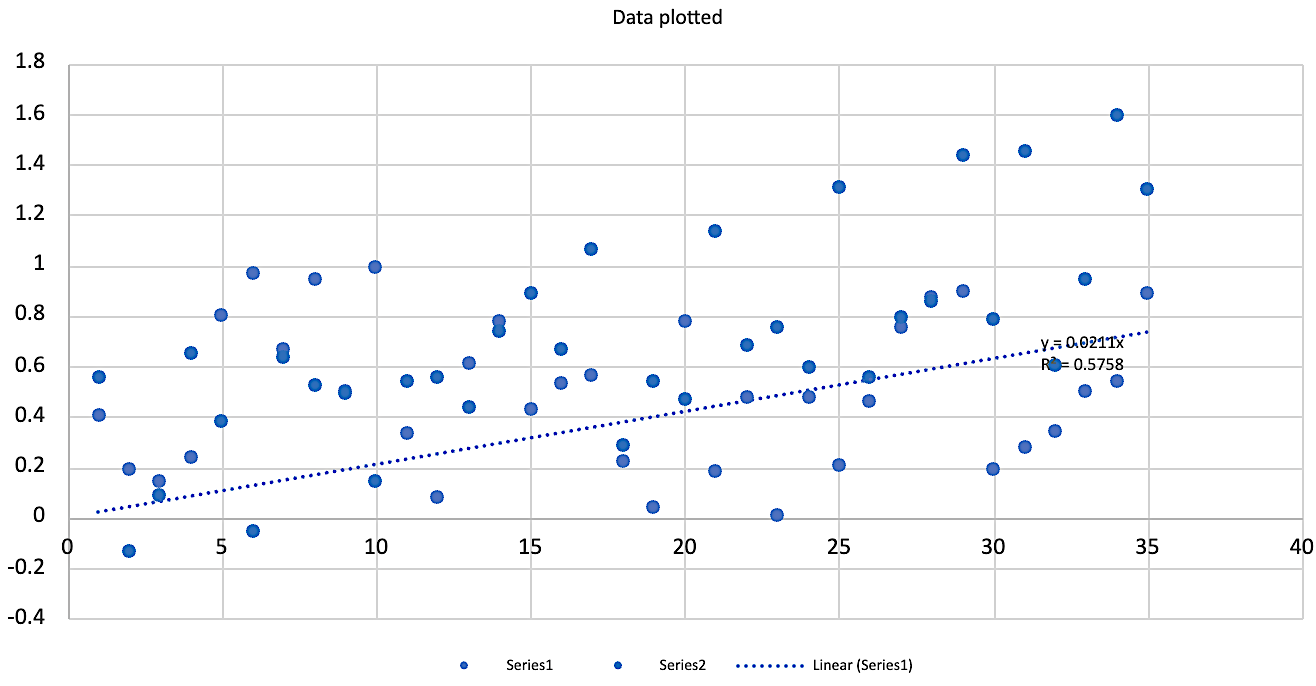
Presenting plots

  • Use descriptive axis labels with units.
  • Choose appropriate plot type.
    • Data points - Scatter plot
    • Line of best-fit (other functions) - line
    • Use different colours so they can be distinguished
  • Include clear legend if needed.
  • Ensure legibility (labels & numbers must be readable, plots should be a suitable size).
  • Include title or caption with equation and $R^2$ (Pearson coefficient) if applicable.


Example (Good) ✅


Example (Bad) ❌


That's all for today!

See you in Week 8!