Quantitative Reasoning

1015SCG

Lecture 11


What is Big Data?

🤔

What is Big Data?

Big Data refers to extremely large and complex datasets that traditional data-processing tools cannot handle efficiently.

  • Generated continuously from digital systems
  • Too large for a single computer to process
  • Requires distributed storage and computing

Big Data is about scale, speed, and complexity.


The 5 Vs of Big Data

Big Data is commonly characterised by five key dimensions:

  • Volume – Massive amounts of data
  • Velocity – Data generated and processed rapidly
  • Variety – Multiple data formats (text, images, video, logs)
  • Veracity – Data uncertainty and quality issues
  • Value – The ability to extract meaningful insights

Managing all five dimensions is central to modern data-driven systems.


Real-World Examples of Big Data

Big Data appears in many industries and everyday technologies:

  • Social Media – Billions of posts, images, and interactions generated daily
  • Streaming Services – Analysing user behaviour to recommend movies and shows
  • Finance – Real-time fraud detection across millions of transactions
  • Large Language Models (LLMs) – Trained on massive and diverse text datasets to learn language patterns and knowledge

Big Data helps organisations make faster and more informed decisions.



From Big Data to Data Science

Big Data focuses on storing and processing massive datasets.

Data Science focuses on extracting meaning and insight from those datasets.

  • Big Data → Infrastructure and scale
  • Data Science → Analysis and prediction
  • Together → Evidence-based decision making

Big Data provides the raw material. Data Science turns it into knowledge.


A brief intro to R

What is R?

R is a programming language for:

  • Statistical computing
  • Data analysis
  • Data visualisation

It is widely used in:

  • Statistics
  • Data science
  • Scientific research
  • Education

R is open-source
and free! 😀

rdrr.io



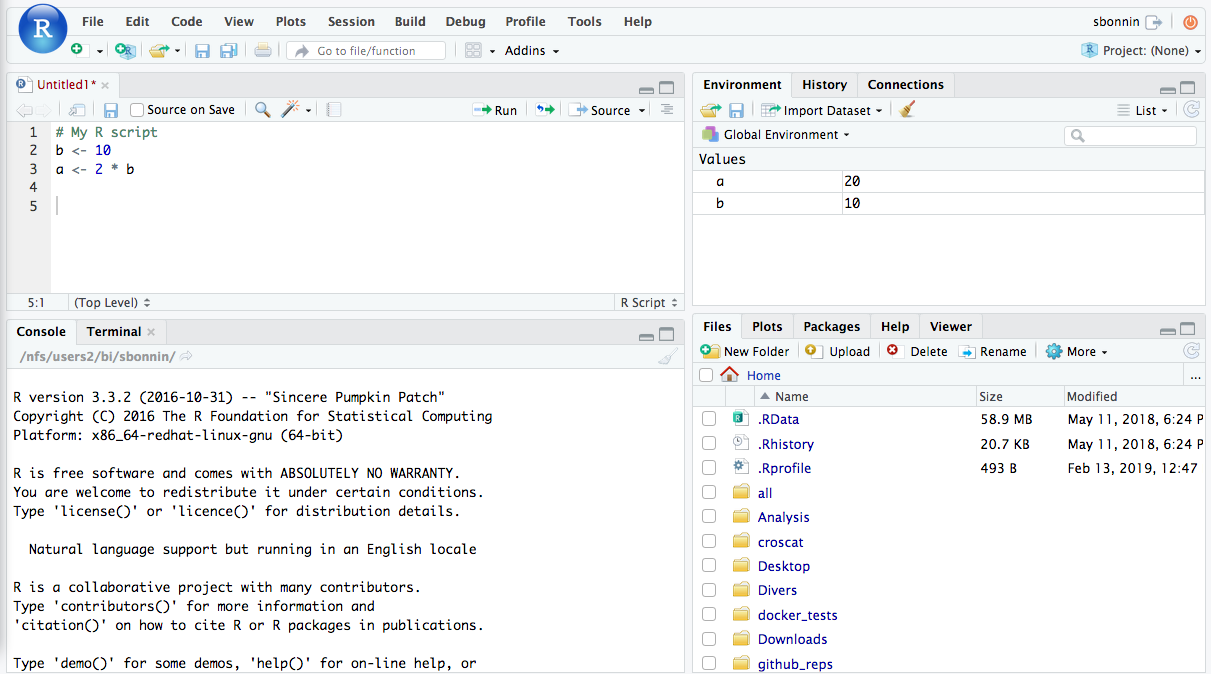
R studio



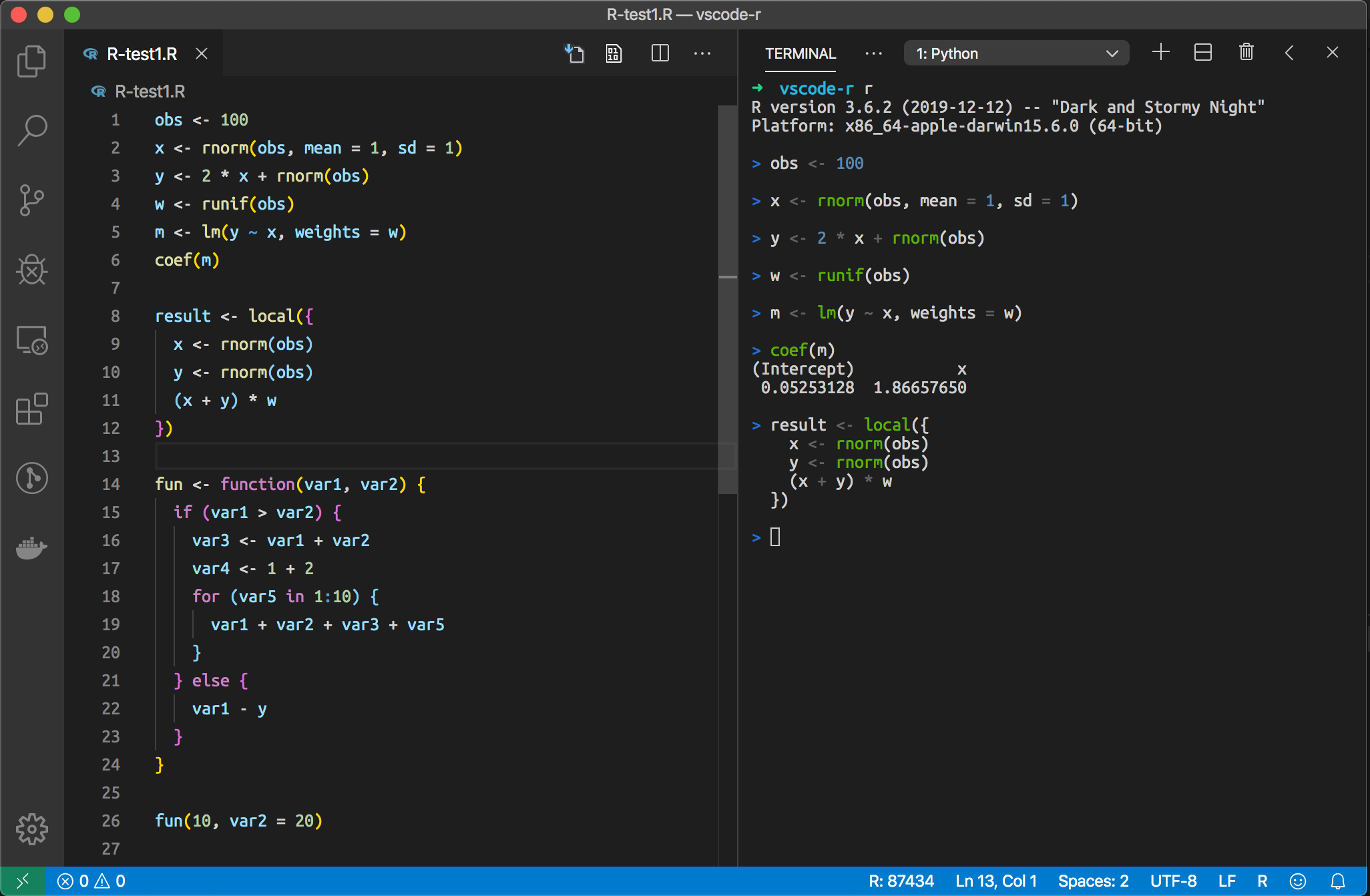
R in Visual Studio Code


Basic R Syntax

Code Output 

# Assign values using <-
x <- 5
y <- 2
        

# Basic arithmetic
x + y
x * y
x / y
> 7
> 10
> 2.5 

# Create a vector
v <- c(1, 2, 3, 4, 5)
mean(v)
> 3



Using cat() in R


Using cat() in R

Code Output 

# Print text and numbers together
x <- 7
y <- -3
cat("x =", x, "and y =", y)
x = 7 and y = -3 

# Control spacing and new lines
cat("Mean value:", mean(c(1,2,3)),
    "\nStandard deviation:", sd(c(1,2,3)))
Mean value: 2
Standard deviation: 1 

# Printing a vector without quotes
v <- c(-3, 1, 7, 3, -5)
cat("Vector v =", v)
Vector v = -3 1 7 3 -5


Working with Data

Code Output 

# Create a data frame
data <- data.frame(
  time = c(1, 2, 3, 4),
  value = c(10, 12, 15, 20)
)


# View data
data
summary(data)

# Simple plot
plot(data$time, data$value)




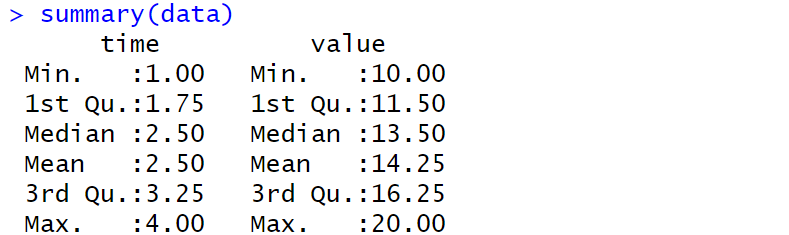
📖 Documentation





R code

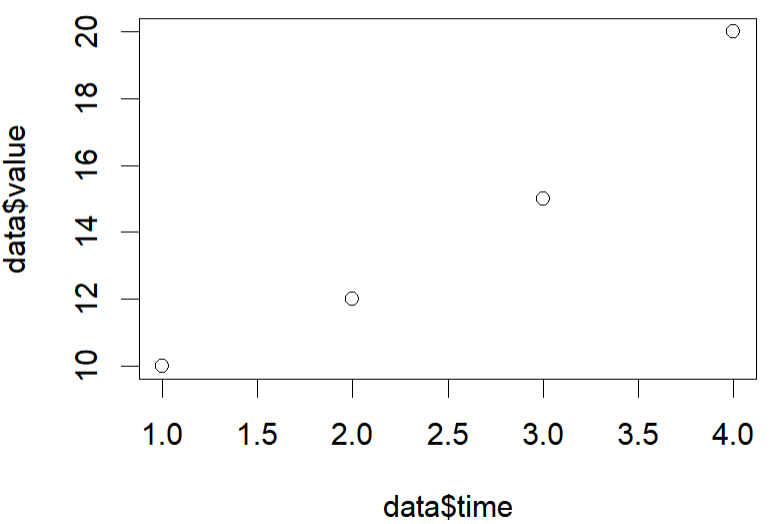
Include data manually

rdrr.io

Scatter plot
 
						# -------------------------
# Data (entered directly)
# -------------------------
# Time variable
time <- c(
  0.246, 0.492, 0.738, 0.984, 1.23, 1.476, 1.722, 1.968, 2.214, 2.46,
  2.706, 2.952, 3.198, 3.444, 3.69, 3.936, 4.182, 4.428, 4.674, 4.92,
  5.166, 5.412, 5.658, 5.904, 6.15, 6.396, 6.642, 6.888, 7.134, 7.38,
  7.626, 7.872, 8.118, 8.364, 8.61, 8.856, 9.102, 9.348, 9.594, 9.84
)
# Activity variable
activity <- c(
  908.3475159, 788.1263257, 668.9006718, 554.6124143, 521.6023327,
  392.2851028, 406.7494851, 323.1341532, 282.4183865, 236.0078351,
  200.7706532, 199.8517187, 169.289558, 148.5259409, 127.8568286,
  98.33976068, 87.93068585, 87.27796212, 73.97245838, 66.69058729,
  56.82525099, 50.73912403, 39.4075143, 34.33557193, 32.61742786,
  25.96560655, 22.36805436, 19.64146032, 16.71665582, 14.63554653,
  12.49930957, 12.4940735, 9.520718439, 8.135601522, 7.562147198,
  6.250336563, 5.376122231, 4.91574392, 4.449048126, 3.892785478
)

# -------------------------
# Scatter plot
# -------------------------
plot(time, activity,
     pch = 19,                        # Solid circular plotting symbol
     cex = 1.5,                       # Size of the plotting points
     col = rgb(0, 0, 0.7, 0.7),       # Blue colour with transparency
     xlab = "time [sec]",             # Label for the x-axis
     ylab = "activity [decays/sec]",  # Label for the y-axis
     main = "Radioactive decay data", # Title of the plot
     las = 1)                         # Axis labels drawn horizontally

grid()                                # Add a background grid to the plot
Scatter plot & Trending line
						# -------------------------
# Data (entered directly)
# -------------------------
# Time variable
x <- c(
  0.246, 0.492, 0.738, 0.984, 1.23, 1.476, 1.722, 1.968, 2.214, 2.46,
  2.706, 2.952, 3.198, 3.444, 3.69, 3.936, 4.182, 4.428, 4.674, 4.92,
  5.166, 5.412, 5.658, 5.904, 6.15, 6.396, 6.642, 6.888, 7.134, 7.38,
  7.626, 7.872, 8.118, 8.364, 8.61, 8.856, 9.102, 9.348, 9.594, 9.84
)
# Activity variable
y <- c(
  908.3475159, 788.1263257, 668.9006718, 554.6124143, 521.6023327,
  392.2851028, 406.7494851, 323.1341532, 282.4183865, 236.0078351,
  200.7706532, 199.8517187, 169.289558, 148.5259409, 127.8568286,
  98.33976068, 87.93068585, 87.27796212, 73.97245838, 66.69058729,
  56.82525099, 50.73912403, 39.4075143, 34.33557193, 32.61742786,
  25.96560655, 22.36805436, 19.64146032, 16.71665582, 14.63554653,
  12.49930957, 12.4940735, 9.520718439, 8.135601522, 7.562147198,
  6.250336563, 5.376122231, 4.91574392, 4.449048126, 3.892785478
)

# Provide reasonable starting values for the parameters
start_vals <- list(
  A = max(y),    # initial activity (approximate)
  k = -0.5       # decay constant (negative for decay)
)

# Fit exponential decay model y = A * exp(kx)
nls_fit <- nls(y ~ A * exp(k * x), start = start_vals)

# Extract fitted parameters
coef_fit <- coef(nls_fit)
A <- coef_fit["A"]
k <- coef_fit["k"]

# Confidence intervals for parameters
conf <- confint(nls_fit)

# Approximate standard errors (1σ) from 95% confidence intervals
A_err <- (conf["A", 2] - conf["A", 1]) / 4
k_err <- (conf["k", 2] - conf["k", 1]) / 4


# -------------------------
# Fitted curves
# -------------------------
# Best-fit curve
y_fit <- A * exp(k * x)
# ±4σ uncertainty envelopes
y_fit_upper <- (A + 4 * A_err) * exp((k + 4 * k_err) * x)
y_fit_lower <- (A - 4 * A_err) * exp((k - 4 * k_err) * x)


# -------------------------
# Plot
# -------------------------
plot(x, y,
     pch = 19,
     cex = 1.5,
     col = rgb(0, 0, 0.7, 0.7),
     xlab = "time [sec]",
     ylab = "activity [decays/sec]",
     main = "Exponential decay fit (nls) with ±4σ",
     las = 1)

grid()

lines(x, y_fit, col = "red", lwd = 2)
lines(x, y_fit_upper, col = "blue", lty = 2, lwd = 1.5)
lines(x, y_fit_lower, col = "blue", lty = 2, lwd = 1.5)

legend("topright",
       legend = c("Data", "Best fit", "±4σ"),
       col = c(rgb(0,0,0.7,0.7), "red", "blue"),
       pch = c(19, NA, NA),
       lty = c(NA, 1, 2),
       lwd = c(NA, 2, 1.5),
       bty = "n")


# -------------------------
# Output results
# -------------------------
cat("Exponential model (nls):\n")
cat(sprintf("A(t) = %.3f * exp(%.4f * t)\n", A, k))
cat(sprintf("Estimated ±1σ: A = %.3f ± %.3f, k = %.4f ± %.4f\n",
            A, A_err, k, k_err))

# Value of the fitted model at t = 0
t0 <- 0
A0 <- A * exp(k * t0)
cat(sprintf("A(0) = %.3f\n", A0))
Linearisation
						# -------------------------
# Data (entered directly)
# -------------------------
t <- c(
  0.246, 0.492, 0.738, 0.984, 1.23, 1.476, 1.722, 1.968, 2.214, 2.46,
  2.706, 2.952, 3.198, 3.444, 3.69, 3.936, 4.182, 4.428, 4.674, 4.92,
  5.166, 5.412, 5.658, 5.904, 6.15, 6.396, 6.642, 6.888, 7.134, 7.38,
  7.626, 7.872, 8.118, 8.364, 8.61, 8.856, 9.102, 9.348, 9.594, 9.84
)

y <- c(
  908.3475159, 788.1263257, 668.9006718, 554.6124143, 521.6023327,
  392.2851028, 406.7494851, 323.1341532, 282.4183865, 236.0078351,
  200.7706532, 199.8517187, 169.289558, 148.5259409, 127.8568286,
  98.33976068, 87.93068585, 87.27796212, 73.97245838, 66.69058729,
  56.82525099, 50.73912403, 39.4075143, 34.33557193, 32.61742786,
  25.96560655, 22.36805436, 19.64146032, 16.71665582, 14.63554653,
  12.49930957, 12.4940735, 9.520718439, 8.135601522, 7.562147198,
  6.250336563, 5.376122231, 4.91574392, 4.449048126, 3.892785478
)

# -------------------------
# Linearisation: ln(y) = ln(A) + k*t
# -------------------------
lny <- log(y)
lin_fit <- lm(lny ~ t)

# Regression parameters
k <- coef(lin_fit)[2]
lnA <- coef(lin_fit)[1]
A <- exp(lnA)

# Standard errors
se <- summary(lin_fit)$coefficients[, "Std. Error"]
k_err <- se[2]
lnA_err <- se[1]
A_err <- A * lnA_err  # propagated error

# R-squared
r_squared <- summary(lin_fit)$r.squared

# Fitted line
lny_fit <- lnA + k * t
y_fit <- A * exp(k * t)

# -------------------------
# Standard error of regression
# -------------------------
n <- length(t)
residuals <- lny - lny_fit
s <- sqrt(sum(residuals^2) / (n - 2))
t_mean <- mean(t)
Sxx <- sum((t - t_mean)^2)
k_err_alt <- s / sqrt(Sxx)
lnA_err_alt <- s * sqrt(1/n + t_mean^2 / Sxx)

# -------------------------
# Plot
# -------------------------
plot(t, lny,
     pch = 19, cex = 1.5, col = rgb(0,0,0.7,0.7),
     xlab = "t [s]",
     ylab = "ln(y) [ln(decays/sec)]",
     main = "Linearised exponential decay with regression",
     las = 1)
grid()
lines(t, lny_fit, col = "red", lwd = 2)
legend("topright",
       legend = c("Linearised data", "Best fit line"),
       col = c(rgb(0,0,0.7,0.7), "red"),
       pch = c(19, NA),
       lty = c(NA, 1),
       lwd = c(NA, 2),
       bty = "n")

# -------------------------
# Half-life computation
# -------------------------
t_half <- log(2) / -k
t_half_err <- log(2) / k^2 * k_err

# -------------------------
# Prediction at t = 5.535 s
# -------------------------
t_pred <- 5.535
sigma_A <- A * lnA_err
sigma_y <- sqrt( (exp(k*t_pred) * sigma_A)^2 + (A * t_pred * exp(k*t_pred) * k_err)^2 )
y_pred <- A * exp(k * t_pred)

# -------------------------
# Output results
# -------------------------
cat("-----------------------\n")
cat("Linearised Model with Uncertainty\n")
cat("-----------------------\n")
cat(sprintf("ln(y) = (%.4f ± %.4f) * t + (%.4f ± %.4f)\n", k, k_err, lnA, lnA_err))
cat(sprintf("R² = %.4f\n", r_squared))
cat(sprintf("Standard error of regression = %.4f\n", s))
cat(sprintf("A = %.4f ± %.4f\n\n", A, A_err))

cat("-----------------------\n")
cat("Exponential Model\n")
cat("-----------------------\n")
cat(sprintf("y = %.4f * exp(%.4f * t)\n\n", A, k))

cat("-----------------------\n")
cat(sprintf("Prediction at t = %.3f s:\n", t_pred))
cat(sprintf("y = %.4f ± %.4f\n\n", y_pred, sigma_y))

cat("-----------------------\n")
cat(sprintf("Half-life t_1/2 = %.4f ± %.4f\n", t_half, t_half_err))
One Sample Student t-test
						# -------------------------
# Data
# -------------------------
data <- c(275.0266497, 255.0311768, 293.8473708, 267.1938408, 242.3487616)
mu0 <- 246.966  # hypothesised mean

# -------------------------
# One-sample t-test
# -------------------------
t_test <- t.test(data, mu = mu0)

# Extract t-statistic
t_stat <- t_test$statistic

# Degrees of freedom
df <- t_test$parameter

# Two-tailed t-critical value (alpha = 0.02)
alpha <- 0.02
t_critical <- qt(1 - alpha/2, df)

# -------------------------
# Output results
# -------------------------
cat("t-statistic:", t_stat, "\n")
cat("t-critical (two-tailed, alpha = 0.02):", t_critical, "\n")

R code

Load data from local folder

Use R-Studio or VScode

Scatter plot
						# -------------------------
# Load data
# -------------------------
getwd()          # Display the current working directory
list.files()     # List all files in the current working directory

# Set the working directory to the folder containing decay3.csv
setwd("C:/Users/YourUserName/Folder/R-code")

# Read the CSV file into a data frame
data <- read.csv("decay3.csv")

# Show the data in the csv file
View(data)

# Extract the first column (time values)
time <- data[[1]]

# Extract the second column (activity values)
activity <- data[[2]]

# -------------------------
# Scatter plot
# -------------------------

plot(time, activity,
     pch = 19,                        # Solid circular plotting symbol
     cex = 1.5,                       # Size of the plotting points
     col = rgb(0, 0, 0.7, 0.7),       # Blue colour with transparency
     xlab = "time [sec]",             # Label for the x-axis
     ylab = "activity [decays/sec]",  # Label for the y-axis
     main = "Radioactive decay data", # Title of the plot
     las = 1)                         # Axis labels drawn horizontally

grid()                                # Add a background grid to the plot
Scatter plot & Trending line
						# -------------------------
# Load data
# -------------------------
getwd()          # Show current working directory (diagnostic)
list.files()     # Show files in the current working directory

# Set working directory to where decay3.csv is stored
setwd("C:/Users/YourUserName/Folder/R-code")

# Read the CSV file into a data frame
data <- read.csv("decay3.csv")

# Assign columns to variables used in the model
x <- data[[1]]   # time values
y <- data[[2]]   # activity values


# -------------------------
# Non-linear fit using nls
# -------------------------
# Provide reasonable starting values for the parameters
start_vals <- list(
  A = max(y),    # initial activity (approximate)
  k = -0.5       # decay constant (negative for decay)
)
# Fit exponential decay model y = A * exp(kx)
nls_fit <- nls(y ~ A * exp(k * x), start = start_vals)
# Extract fitted parameters
coef_fit <- coef(nls_fit)
A <- coef_fit["A"]
k <- coef_fit["k"]
# Confidence intervals for parameters
conf <- confint(nls_fit)
# Approximate standard errors (1σ) from 95% confidence intervals
A_err <- (conf["A", 2] - conf["A", 1]) / 4
k_err <- (conf["k", 2] - conf["k", 1]) / 4


# -------------------------
# Fitted curves
# -------------------------
# Best-fit curve
y_fit <- A * exp(k * x)
# ±4σ uncertainty envelopes
y_fit_upper <- (A + 4 * A_err) * exp((k + 4 * k_err) * x)
y_fit_lower <- (A - 4 * A_err) * exp((k - 4 * k_err) * x)


# -------------------------
# Plot
# -------------------------
plot(x, y,
     pch = 19,
     cex = 1.5,
     col = rgb(0, 0, 0.7, 0.7),
     xlab = "time [sec]",
     ylab = "activity [decays/sec]",
     main = "Exponential decay fit (nls) with ±4σ",
     las = 1)

grid()

lines(x, y_fit, col = "red", lwd = 2)
lines(x, y_fit_upper, col = "blue", lty = 2, lwd = 1.5)
lines(x, y_fit_lower, col = "blue", lty = 2, lwd = 1.5)

legend("topright",
       legend = c("Data", "Best fit", "±4σ"),
       col = c(rgb(0,0,0.7,0.7), "red", "blue"),
       pch = c(19, NA, NA),
       lty = c(NA, 1, 2),
       lwd = c(NA, 2, 1.5),
       bty = "n")


# -------------------------
# Output results
# -------------------------
cat("Exponential model (nls):\n")
cat(sprintf("A(t) = %.3f * exp(%.4f * t)\n", A, k))
cat(sprintf("Estimated ±1σ: A = %.3f ± %.3f, k = %.4f ± %.4f\n",
            A, A_err, k, k_err))

# Value of the fitted model at t = 0
t0 <- 0
A0 <- A * exp(k * t0)
cat(sprintf("A(0) = %.3f\n", A0))
Linearisation
						# -------------------------
# Load data
# -------------------------
getwd()          # Display current working directory (diagnostic)
list.files()     # List files in the current working directory

# Set working directory to the folder containing decay3.csv
setwd("C:/Users/YourUserName/Folder/R-code")

# Read the CSV file into a data frame
data <- read.csv("decay3.csv", header = TRUE)

# -------------------------
# Extract columns safely
# -------------------------
# If the CSV file has column names "time" and "activity",
# use them; otherwise, assume the first two columns

if (!("time" %in% colnames(data)) | !("activity" %in% colnames(data))) {
  time <- data[, 1]      # first column: time
  activity <- data[, 2]  # second column: activity
} else {
  time <- data$time
  activity <- data$activity
}

# -------------------------
# Linearisation: ln(y) = ln(A) + k t
# -------------------------
# Take the natural logarithm of the activity data
lny <- log(activity)

# Perform linear regression on the linearised model
lin_fit <- lm(lny ~ time)

# -------------------------
# Extract regression parameters
# -------------------------
k   <- coef(lin_fit)[2]   # slope (decay constant)
lnA <- coef(lin_fit)[1]   # intercept
A   <- exp(lnA)           # recover A from ln(A)

# -------------------------
# Parameter uncertainties
# -------------------------
# Standard errors from regression output
se <- summary(lin_fit)$coefficients[, "Std. Error"]

k_err   <- se[2]          # uncertainty in k
lnA_err <- se[1]          # uncertainty in ln(A)

# Propagate uncertainty from ln(A) to A
A_err <- A * lnA_err

# -------------------------
# Goodness of fit
# -------------------------
r_squared <- summary(lin_fit)$r.squared

# -------------------------
# Fitted models
# -------------------------
# Linearised fitted line
lny_fit <- lnA + k * time

# Corresponding exponential model
y_fit <- A * exp(k * time)

# -------------------------
# Standard error of regression
# -------------------------
n <- length(time)                 # number of data points
residuals <- lny - lny_fit        # residuals of linearised fit

# Standard error of the regression
s <- sqrt(sum(residuals^2) / (n - 2))

# Alternative expressions for parameter uncertainties
t_mean <- mean(time)
Sxx <- sum((time - t_mean)^2)

k_err_alt   <- s / sqrt(Sxx)
lnA_err_alt <- s * sqrt(1 / n + t_mean^2 / Sxx)

# -------------------------
# Plot (force refresh)
# -------------------------
graphics.off()   # Close any existing graphics device

plot(time, lny,
     pch = 19,
     cex = 1.5,
     col = rgb(0, 0, 0.7, 0.7),
     xlab = "t [s]",
     ylab = "ln(y) [ln(decays/sec)]",
     main = "Linearised exponential decay with regression",
     las = 1)

grid()
lines(time, lny_fit, col = "red", lwd = 2)

legend("topright",
       legend = c("Linearised data", "Best fit line"),
       col = c(rgb(0,0,0.7,0.7), "red"),
       pch = c(19, NA),
       lty = c(NA, 1),
       lwd = c(NA, 2),
       bty = "n")

# -------------------------
# Half-life computation
# -------------------------
# Half-life for exponential decay: t_1/2 = ln(2)/|k|
t_half <- log(2) / -k

# Uncertainty in half-life (propagation)
t_half_err <- log(2) / k^2 * k_err

# -------------------------
# Prediction at a specific time
# -------------------------
t_pred <- 5.535

# Propagate uncertainty in A and k
sigma_A <- A * lnA_err
sigma_y <- sqrt(
  (exp(k * t_pred) * sigma_A)^2 +
    (A * t_pred * exp(k * t_pred) * k_err)^2
)

# Predicted activity
y_pred <- A * exp(k * t_pred)

# -------------------------
# Output results
# -------------------------
cat("-----------------------\n")
cat("Linearised Model with Uncertainty\n")
cat("-----------------------\n")
cat(sprintf("ln(y) = (%.4f ± %.4f) t + (%.4f ± %.4f)\n",
            k, k_err, lnA, lnA_err))
cat(sprintf("R² = %.4f\n", r_squared))
cat(sprintf("Standard error of regression = %.4f\n", s))
cat(sprintf("A = %.4f ± %.4f\n\n", A, A_err))

cat("-----------------------\n")
cat("Exponential Model\n")
cat("-----------------------\n")
cat(sprintf("y = %.4f * exp(%.4f t)\n\n", A, k))

cat("-----------------------\n")
cat(sprintf("Prediction at t = %.3f s:\n", t_pred))
cat(sprintf("y = %.4f ± %.4f\n\n", y_pred, sigma_y))

cat("-----------------------\n")
cat(sprintf("Half-life t_1/2 = %.4f ± %.4f\n", t_half, t_half_err))
One Sample Student t-test
						# -------------------------
# Data
# -------------------------
# Sample data (observed measurements)
data <- c(275.0266497, 255.0311768, 293.8473708, 267.1938408, 242.3487616)

# Hypothesised population mean under H0
mu0 <- 246.966

# -------------------------
# One-sample t-test
# -------------------------

# Perform a one-sample Student t-test:
# H0: true mean = mu0
# H1: true mean ≠ mu0 (two-tailed by default)
t_test <- t.test(data, mu = mu0)

# Extract the t-statistic from the test result
t_stat <- t_test$statistic

# Degrees of freedom (n - 1 for one-sample t-test)
df <- t_test$parameter

# -------------------------
# Critical value
# -------------------------

# Significance level (alpha = 0.02 corresponds to a 98% confidence level)
alpha <- 0.02

# Two-tailed critical t-value:
# used for rejection region |t| > t_critical
t_critical <- qt(1 - alpha / 2, df)

# -------------------------
# Output results
# -------------------------

cat("t-statistic:", t_stat, "\n")
cat("t-critical (two-tailed, alpha = 0.02):", t_critical, "\n")

Python code

Include data manually

trinket.io/Python3

Scatter plot
						import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# -------------------------
# Data (entered directly)
# -------------------------
time = np.array([
    0.246, 0.492, 0.738, 0.984, 1.23, 1.476, 1.722, 1.968, 2.214, 2.46,
    2.706, 2.952, 3.198, 3.444, 3.69, 3.936, 4.182, 4.428, 4.674, 4.92,
    5.166, 5.412, 5.658, 5.904, 6.15, 6.396, 6.642, 6.888, 7.134, 7.38,
    7.626, 7.872, 8.118, 8.364, 8.61, 8.856, 9.102, 9.348, 9.594, 9.84
])

activity = np.array([
    908.3475159, 788.1263257, 668.9006718, 554.6124143, 521.6023327,
    392.2851028, 406.7494851, 323.1341532, 282.4183865, 236.0078351,
    200.7706532, 199.8517187, 169.289558, 148.5259409, 127.8568286,
    98.33976068, 87.93068585, 87.27796212, 73.97245838, 66.69058729,
    56.82525099, 50.73912403, 39.4075143, 34.33557193, 32.61742786,
    25.96560655, 22.36805436, 19.64146032, 16.71665582, 14.63554653,
    12.49930957, 12.4940735, 9.520718439, 8.135601522, 7.562147198,
    6.250336563, 5.376122231, 4.91574392, 4.449048126, 3.892785478
])

# -------------------------
# Scatter plot
# -------------------------
plt.figure(figsize=(6, 4))
plt.scatter(time, activity, s=40, alpha=0.7)

plt.xlabel("time [sec]")
plt.ylabel("activity [decays/sec]")
plt.title("Radioactive decay data")
plt.grid(True)
plt.show()
Scatter plot & Trending line
						import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# -------------------------
# Data (entered directly)
# -------------------------
x = np.array([
    0.246, 0.492, 0.738, 0.984, 1.23, 1.476, 1.722, 1.968, 2.214, 2.46,
    2.706, 2.952, 3.198, 3.444, 3.69, 3.936, 4.182, 4.428, 4.674, 4.92,
    5.166, 5.412, 5.658, 5.904, 6.15, 6.396, 6.642, 6.888, 7.134, 7.38,
    7.626, 7.872, 8.118, 8.364, 8.61, 8.856, 9.102, 9.348, 9.594, 9.84
])

y = np.array([
    908.3475159, 788.1263257, 668.9006718, 554.6124143, 521.6023327,
    392.2851028, 406.7494851, 323.1341532, 282.4183865, 236.0078351,
    200.7706532, 199.8517187, 169.289558, 148.5259409, 127.8568286,
    98.33976068, 87.93068585, 87.27796212, 73.97245838, 66.69058729,
    56.82525099, 50.73912403, 39.4075143, 34.33557193, 32.61742786,
    25.96560655, 22.36805436, 19.64146032, 16.71665582, 14.63554653,
    12.49930957, 12.4940735, 9.520718439, 8.135601522, 7.562147198,
    6.250336563, 5.376122231, 4.91574392, 4.449048126, 3.892785478
])

# -------------------------
# Linearisation
# ln(y) = ln(A) + kx
# -------------------------
lny = np.log(y)

# Linear regression using scipy.stats
result = stats.linregress(x, lny)

k = result.slope
lnA = result.intercept
A = np.exp(lnA)

r_value = result.rvalue
r_squared = r_value**2

# Standard errors
k_err = result.stderr
lnA_err = result.intercept_stderr
A_err = A * lnA_err   # error propagation

# -------------------------
# Fitted curve
# -------------------------
y_fit = A * np.exp(k * x)

# -------------------------
# Error curves (±1σ)
# -------------------------
y_fit_upper = (A + 4 * A_err) * np.exp((k + 4 * k_err) * x)
y_fit_lower = (A - 4 * A_err) * np.exp((k - 4 * k_err) * x)


# -------------------------
# Plot
# -------------------------
plt.figure(figsize=(6, 4))

plt.scatter(x, y, s=40, alpha=0.7, label="Data")
plt.plot(x, y_fit, linewidth=2, label="Best fit")

plt.plot(
    x, y_fit_upper,
    linestyle="--", linewidth=1.5,
    label="Upper fit (+4σ)"
)

plt.plot(
    x, y_fit_lower,
    linestyle="--", linewidth=1.5,
    label="Lower fit (−4σ)"
)

plt.xlabel("time [sec]")
plt.ylabel("activity [decays/sec]")
plt.title("Exponential decay fit with parameter uncertainty")
plt.legend()
plt.grid(True)
plt.show()


# -------------------------
# Output results
# -------------------------
print("Exponential model:")
print(f"A(t) = A exp(k t)")
print()
print(f"A = {A:.3f} ± {A_err:.3f}")
print(f"k = {k:.4f} ± {k_err:.4f}")
print(f"R² = {r_squared:.4f}")

# Value at t = 0
t0 = 0
A0 = A * np.exp(k * t0)
print(f"A(0) = {A0:.3f}")
Linearisation
						import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# -------------------------
# Data (entered directly)
# -------------------------
t = np.array([
    0.246, 0.492, 0.738, 0.984, 1.23, 1.476, 1.722, 1.968, 2.214, 2.46,
    2.706, 2.952, 3.198, 3.444, 3.69, 3.936, 4.182, 4.428, 4.674, 4.92,
    5.166, 5.412, 5.658, 5.904, 6.15, 6.396, 6.642, 6.888, 7.134, 7.38,
    7.626, 7.872, 8.118, 8.364, 8.61, 8.856, 9.102, 9.348, 9.594, 9.84
])

y = np.array([
    908.3475159, 788.1263257, 668.9006718, 554.6124143, 521.6023327,
    392.2851028, 406.7494851, 323.1341532, 282.4183865, 236.0078351,
    200.7706532, 199.8517187, 169.289558, 148.5259409, 127.8568286,
    98.33976068, 87.93068585, 87.27796212, 73.97245838, 66.69058729,
    56.82525099, 50.73912403, 39.4075143, 34.33557193, 32.61742786,
    25.96560655, 22.36805436, 19.64146032, 16.71665582, 14.63554653,
    12.49930957, 12.4940735, 9.520718439, 8.135601522, 7.562147198,
    6.250336563, 5.376122231, 4.91574392, 4.449048126, 3.892785478
])

# -------------------------
# Linearisation: ln(y) = ln(A) + k*t
# -------------------------
lny = np.log(y)

# Linear regression using scipy.stats
result = stats.linregress(t, lny)

k = result.slope
lnA = result.intercept
A = np.exp(lnA)

# Regression statistics
r_value = result.rvalue
r_squared = r_value**2
k_err = result.stderr
lnA_err = result.intercept_stderr
A_err = A * lnA_err  # propagated error

# Fitted line
lny_fit = lnA + k * t
y_fit = A * np.exp(k * t)

# -------------------------
# Standard error of regression
# -------------------------
n = len(t)
residuals = lny - lny_fit
s = np.sqrt(np.sum(residuals**2) / (n - 2))
t_mean = np.mean(t)
Sxx = np.sum((t - t_mean)**2)
k_err_alt = s / np.sqrt(Sxx)
lnA_err_alt = s * np.sqrt(1/n + t_mean**2 / Sxx)

# -------------------------
# Plot
# -------------------------
plt.figure(figsize=(6, 4))
plt.scatter(t, lny, s=40, alpha=0.7, label="Linearised data (ln(y))")
plt.plot(t, lny_fit, linewidth=2, label="Best fit line")
plt.xlabel("t [s]")
plt.ylabel("ln(y) [ln(decays/sec)]")
plt.title("Linearised exponential decay with regression")
plt.legend()
plt.grid(True)
plt.show()

# -------------------------
# Half-life computation
# -------------------------
t_half = np.log(2) / -k
t_half_err = np.log(2) / k**2 * k_err

# -------------------------
# Prediction at t = 5.535 s
# -------------------------
t_pred = 5.535
sigma_A = A * lnA_err
sigma_y = np.sqrt((np.exp(k * t_pred) * sigma_A)**2 + (A * t_pred * np.exp(k * t_pred) * k_err)**2)
y_pred = A * np.exp(k * t_pred)

# -------------------------
# Output results
# -------------------------
print("-----------------------")
print("Linearised Model with Uncertainty")
print("-----------------------")
print(f"ln(y) = ({k:.4f} ± {k_err:.4f}) t + ({lnA:.4f} ± {lnA_err:.4f})")
print(f"R² = {r_squared:.4f}")
print(f"Standard error of regression = {s:.4f}")
print(f"A = {A:.4f} ± {A_err:.4f}")
print()
print("-----------------------")
print("Exponential Model")
print("-----------------------")
print(f"y = {A:.4f} * exp({k:.4f} * t)")
print()
print("-----------------------")
print(f"Prediction at t = {t_pred:.3f} s:")
print(f"y = {y_pred:.4f} ± {sigma_y:.4f}")
print()
print("-----------------------")
print(f"Half-life t_1/2 = {t_half:.4f} ± {t_half_err:.4f}")
print()
One Sample Student t-test
						import numpy as np
from scipy import stats

# Given data
data = np.array([
    275.0266497,	255.0311768,	293.8473708,	267.1938408,	242.3487616
])

mu0 = 246.966  # hypothesised mean

# One-sample t-test
t_stat, p_value = stats.ttest_1samp(data, mu0)

# Degrees of freedom
df = len(data) - 1

# t-critical value (alpha = 0.02, two-tailed)
alpha = 0.02
t_critical = stats.t.ppf(1 - alpha/2, df)

print("t-statistic:", t_stat)
print("t-critical:", t_critical)

That's all for today!

See you next time!