A Brief Story of
$\large \pi$ and $\large e$

A Story of $\large \pi$

A very brief overview

Where does $\large \pi$ come from?

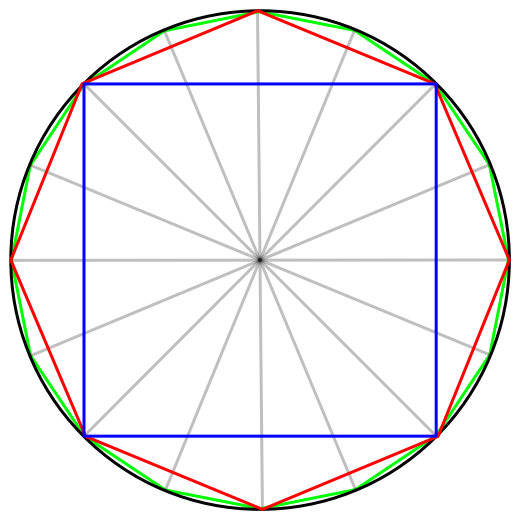
$\Large \pi $ is the ratio of a circle's circumference to its diameter: $\dfrac{C}{D}$


Origin of $\large \pi$

  • Babylonians (~1900-1600 BCE) used Pi $= 3\frac18 = 3.125$.
  • Egyptians (Rhind Papyrus) used Pi $ = \left(\frac{16}{9}\right)^2 = 3.1605$.
  • Archimedes (250 BCE): $\pi$ between $3\frac{10}{71}$ and $3\frac{1}{7}.$
  • Symbol “$\Large \pi$” introduced by William Jones in 1706; adopted by Euler.

Common uses of $\large \pi$ in the past (and nowadays too)

  • Estimating the area of circles in land division, irrigation, architecture and astronomy.

More Common Uses Today

  • Geometry: circle formulas, surface areas, volumes.
  • Trigonometry: sine, cosine, periodic functions.
  • Physics: waves, oscillations, relativity.
  • Engineering: signal processing, simulations, structural analysis.
  • Computer graphics: rotations, animations, transformations.
$V = \dfrac{4}{3}\pi r^2$ $\sin(x),$ $ \cos(x),$
$\tan(x)$ 		$\Lambda =\dfrac{8\pi}{3c^2}\rho$ $X(n) = \ds \sum_{n=0}^{n-1}x(n) e^{-j\frac{2\pi}{N}kn}$


Fun Facts

  • March 14 (3/14) is celebrated as Pi Day around the world.
  • $\large \pi$ is also transcendental — impossible to express as a root of a polynomial.


Fun Facts

  • $\large \pi$ is irrational — its decimal expansion never ends or repeats.

Why $\large \pi$ Matters

A universal constant appearing throughout mathematics,
nature, science, and technology.



A Story of $\large e$

A very brief overview

Origin of $\large e$

  • First appeared in studies of compound interest in the 1600s.

Origin of $\large e$

How compound interest works?

  • Suppose we invest $\$ 100$ in an account that pays 5 percent interest, compounded annually.
Year Computation Amount ($)
1 100 × 1.05 105.00
2 100 × 1.05² = 105 × 1.05 110.25
3 100 × 1.05³ = 110.25 × 1.05 115.76


Origin of $\large e$

How compound interest works?

  • Formula for compound interest: \[ \large S = P\left(1+\dfrac{r}{n}\right)^{nt} \]
  • $P=$ investment in dollars,
  • $r=$ interest (%),
  • $t=$ time in years,
  • $n=$ number of time the compounding is done per year.



Origin of $\large e$

  • Using the formula: \(\,S = P\left(1+\dfrac{r}{n}\right)^{nt}\,\) for $\,P=100.$
Conversion period Computation Amount ($)
Annually 100 × (1 + 0.05/1)1 105.00
Semiannually 100 × (1 + 0.05/2)2 105.06
Quarterly 100 × (1 + 0.05/4)4 105.09
Monthly 100 × (1 + 0.05/12)12 105.12
Weekly 100 × (1 + 0.05/52)52 105.12
Daily 100 × (1 + 0.05/365)365 105.13

Origin of $\large e$

  • \(S = \left(1+\dfrac{1}{n}\right)^{n}\)
  • $P=\$1$
  • $r=1\,$ (100% interest)
  • $t = 1\,$ annually

No bank has ever come up with such a generous offer. ☹️


$n$ Amount
1 2.000000
2 2.250000
3 2.370370
10 2.593742
50 2.691588
100 2.704814
1 000 2.716924
100 000 2.718268
10 000 000 2.718282

Origin of $\large e$

  • Jacob Bernoulli (1683) discovered that when $n$ tends to infinity the value of \( \left(1 + \dfrac{1}{n}\right)^n \) is $\, 2.71828\ldots $ $\approx \Large e$
  • Leonhard Euler (1727/1728) gave the constant its name “$\Large e$” and formalised its properties.

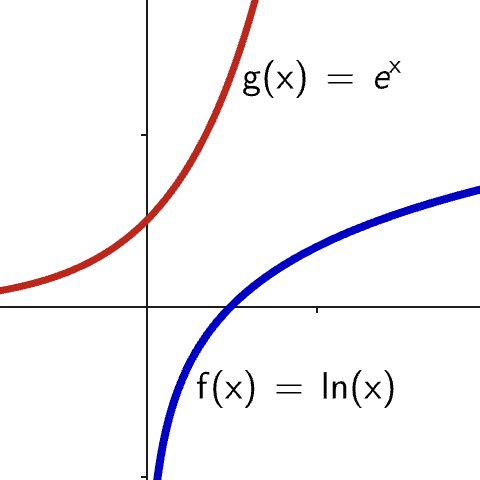
What is $\large e$?

  • $e\approx 2.71828\ldots$ is an irrational and transcendental. 🤯
  • The base of natural logarithms.
  • The unique number for which the derivative of \( e^x \) is itself.


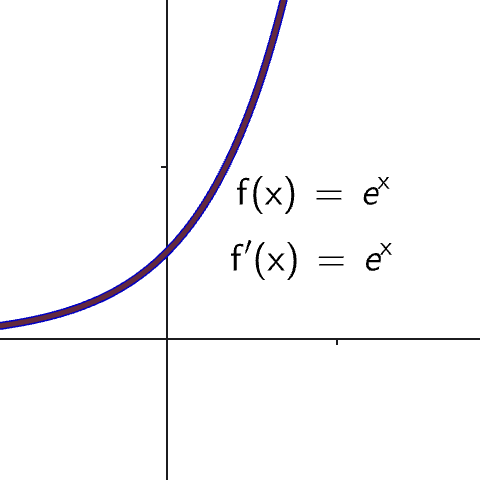Common Uses Today

  • Exponential growth and decay (population 👥, radioactivity ☢️, interest 💵).
  • Calculus: differential equations, integrals, limits.
  • Probability: normal distribution, Poisson processes.
  • Complex analysis: Euler's formula

    A surprising connection with $\,\large 0,$ $\large 1,$ $\LARGE \pi$ and ${\Large i}\large =\sqrt{-1}.$ 🤯




Why $\large e$ Matters

The natural base that describes change, randomness,
and the structure of continuous processes.


References

  • A history of $\Large \pi\,$ by Petr Beckmann
  • $\Large e$ The story of a number by Eli Maor









Design, Images & Applets
Juan Carlos Ponce Campuzano
unless otherwise stated