Foundation Mathematics
1017SCG
Week 6
Topics for Week 6
- Exponential Growth/Decay
- Solving Trigonometric Equations
- Introduction of Functions
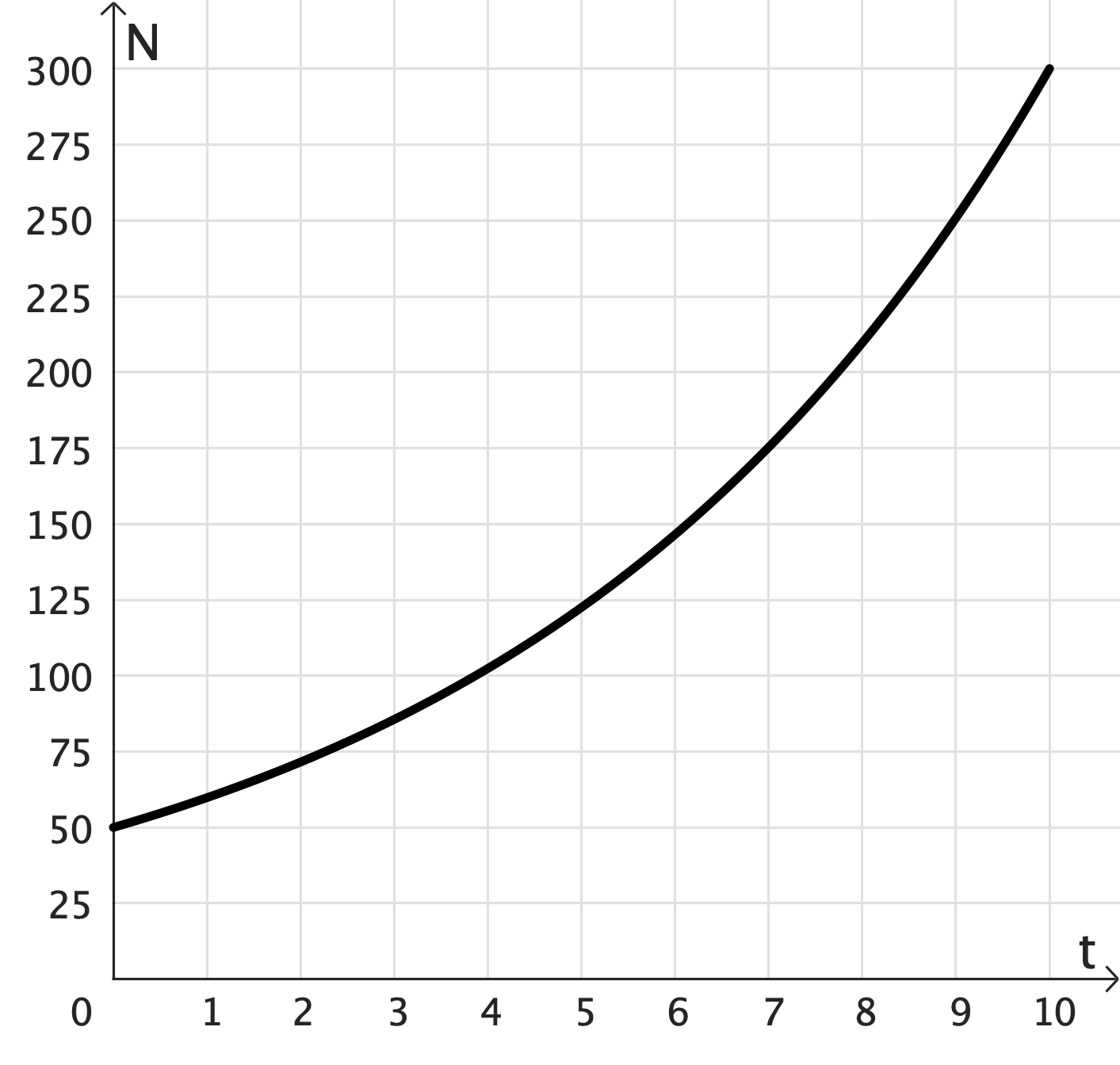
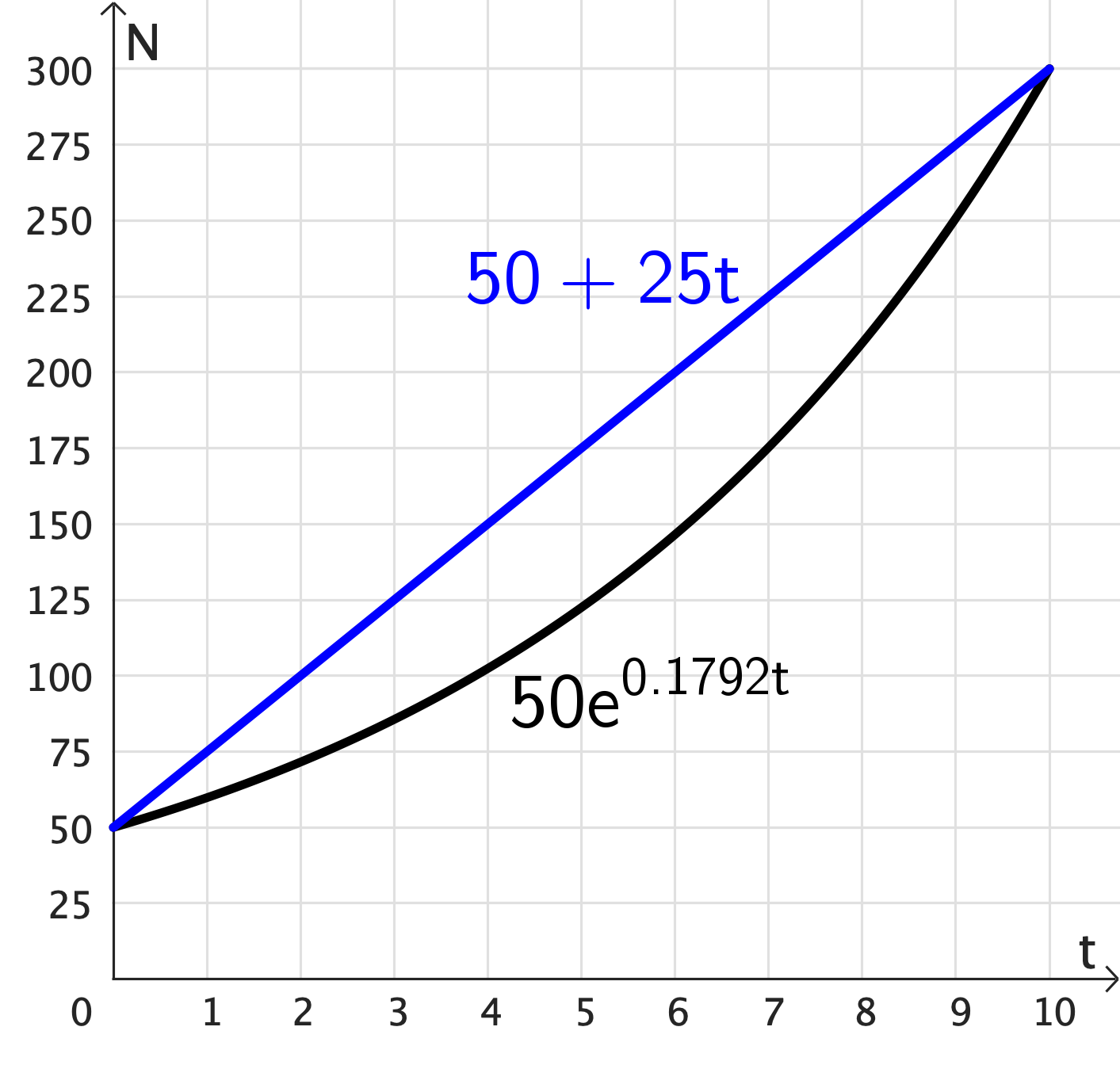
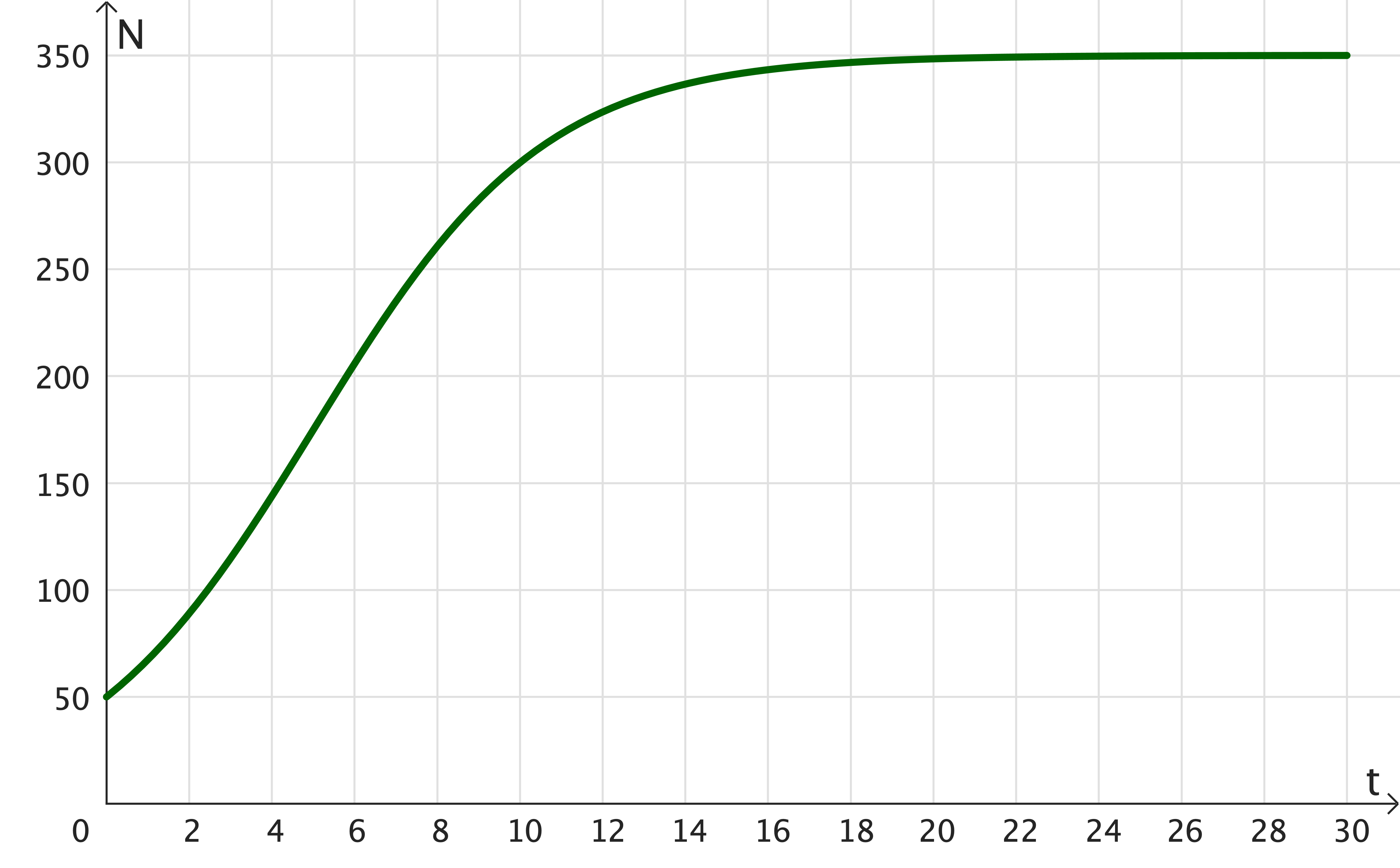
Population Modelling Scenario 🤔
Initially there were 50 animals. After 10 years,
the animal population had increased to 300.
Make a predication of the animal population
after another 5 years has passed.
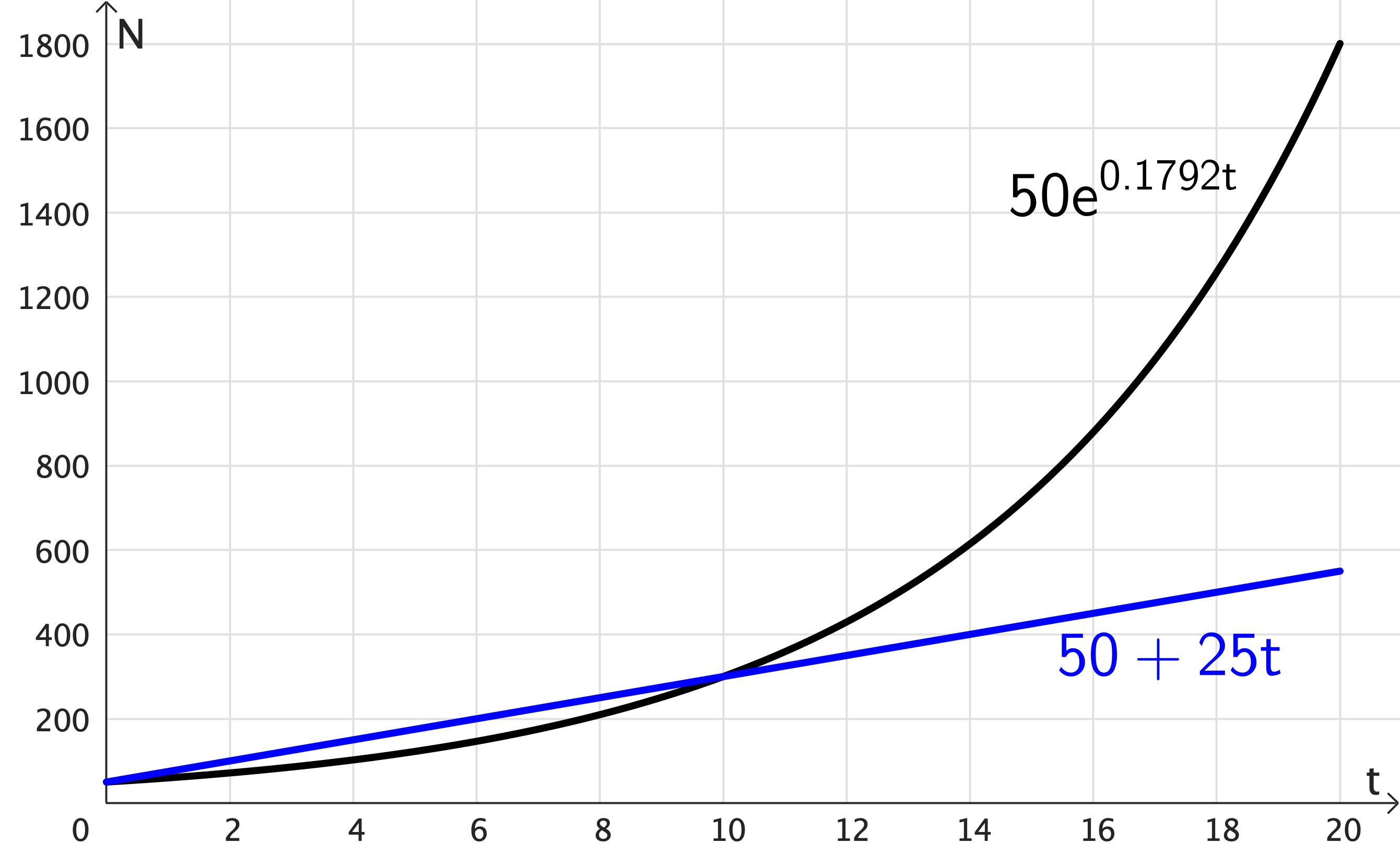
Linear Growth: $N = 50 + 25 t$
|
|
Exponential Growth: $N = 50 e^{0.1792t }$
|
|
Linear vs Exponential Growth
Logistic Growth
Exponential Growth/Decay
\(N = N_0 e^{kt}\)
- $t\,$ is the amount of time that has passed
- $N_0\,$ is the initial amount
- $N\,$ is the amount present at time $t$
- $k\,$ is the growth/decay factor
- $e$ $\approx 2.71828\;\; $ Euler's number
Scenario 1
The population of fish in a pond grows according the exponential growth model
\(N = N_0 e^{kt}.\)
Initially there were 50 fish is the pond. Four weeks later, there were 80 fish in the pond.
Exponential Growth
The population of fish in a pond grows according the exponential growth model
\(N = N_0 e^{kt}.\)
Initially there were 50 fish is the pond. Four weeks later, there were 80 fish in the pond.
- Find the value of the growth factor $k.$
- What is the expected number of fish in the pond after eight weeks?
- When would there be 200 fish in the pond?
Exponential Growth
The population of fish in a pond grows according the exponential growth model
\(N = N_0 e^{kt}.\)
Initially there were 50 fish is the pond. Four weeks later, there were 80 fish in the pond.
• Initial population $N_0=50$
• Time passed $t=4$ (weeks)
• At time $t=4,$ the population $N=80$
Exponential Growth
Data: $\,N_0=50,\;$ $t=4,\;$ $N=80$
• Find the value of the growth factor $k.$
| \(N\) | \(=\) | \( N_0e^{kt}\) |
| \(80\) | \(=\) | \( 50e^{k(4)}\) \(\, = 50e^{4k}\) |
| \(\dfrac{80}{50}\) | \(=\) | \( \dfrac{50e^{4k}}{50}\) |
| \(\dfrac{8}{5}\) | \(=\) | \( e^{4k}\) |
Exponential Growth
Data: $\,N_0=50,\;$ $t=4,\;$ $N=80$
• Find the value of the growth factor $k.$
| \( e^{4k}\) | \(=\) | \(\dfrac{8}{5}\) |
| \(\ln\left(e^{4k}\right)\) | \(=\) | \(\ln\left( \dfrac{8}{5}\right)\) |
| \( 4k=\,\) \(4k \ln\left(e\right)\) | \(=\) | \(\ln\left( \dfrac{8}{5}\right)\) |
| \(k\) | \(=\) | \(\dfrac{1}{4}\ln\left( \dfrac{8}{5}\right)\) \(\,= 0.1175\) |
Exponential Growth
👉 New Data: $\,N_0=50,\;$ $k = 0.1175$
• What is the expected number of fish in the pond after eight weeks?
| \(N\) | \(=\) | \(N_0e^{kt}\) |
| \(N\) | \(=\) | \(50e^{(0.1175)(8)}\) |
| \(N\) | \(=\) | \(50e^{0.94}\) \(\approx 127.99\ldots \) |
| \(N\) | \(=\) | \(128\) fishes |
After 8 weeks, it is predicted that there will be 128 fish in the pond.
Exponential Growth
👉 New Data: $\,N_0=50,\;$ $k = 0.1175$
• When would there be 200 fish in the pond?
| \(N\) | \(=\) | \(N_0e^{kt}\) |
| \(200\) | \(=\) | \(50e^{(0.1175)t}\) |
| \(\dfrac{200}{50}\) | \(=\) | \(\dfrac{50e^{0.1175}}{50}\) |
| \(4\) | \(=\) | \(e^{0.1175 t}\) |
| \(\ln(4)\) | \(=\) | \(\ln\left(e^{0.1175 t}\right)\) |
Exponential Growth
👉 New Data: $\,N_0=50,\;$ $k = 0.1175$
• When would there be 200 fish in the pond?
| \(\ln(4)\) | \(=\) | \(\ln\left(e^{0.1175 t}\right)\) |
| \(\ln(4)\) | \(=\) | \(0.1175 t\) |
| \(\dfrac{\ln(4)}{0.1175}\) | \(=\) | \(\dfrac{0.1175 t}{0.1175}\) |
| \(t\) | \(=\) | \(\dfrac{\ln(4)}{0.1175}\) \(= 11.80\) weeks |
Therefore, it takes a little under 12 weeks for the population of fish to reach 200.
Scenario 2
A radioactive substance decays according to the exponential decay model
\(N = N_0 e^{kt}.\)
Initially, the radioactive substance had a mass of 3 grams. After 200 years, it only had a mass of 2.5 grams.
Note: This is an inaccurate representation of an atom. Learn more about it here
Exponential Decay
A radioactive substance decays according to the exponential decay model
\(N = N_0 e^{kt}.\)
Initially, the radioactive substance had a mass of 3 grams. After 200 years, it only had a mass of 2.5 grams.
- Calculate the decay factor $k.$
- How much of the radioactive substance would be left after 400 years?
- What is the half-life of the radioactive substance?
Exponential Decay
A radioactive substance decays according to the exponential decay model
\(N = N_0 e^{kt}.\)
Initially, the radioactive substance had a mass of 3 grams. After 200 years, it only had a mass of 2.5 grams.
• Initial mass $N_0=3$
• Time passed $t=100$ (years)
• At time $t=200,$ the mass is $N=2.5$
Exponential Decay
Data: $\,N_0=3,\;$ $t=200,\;$ $N=2.5$
• Calculate the decay factor $k.$
| \(N\) | \(=\) | \( N_0e^{kt}\) |
| \(2.5\) | \(=\) | \( 3e^{k(200)}\) \(\, = 3e^{200k}\) |
| \(\dfrac{2.5}{3}\) | \(=\) | \( \dfrac{3e^{200k}}{3}\) |
| \(\dfrac{2.5}{3}\) | \(=\) | \( e^{200k}\) |
Exponential Decay
Data: $\,N_0=3,\;$ $t=200,\;$ $N=2.5$
• Calculate the decay factor $k.$
| \( e^{200k}\) | \(=\) | \(\dfrac{2.5}{3}\) |
| \(\ln\left(e^{200k}\right)\) | \(=\) | \(\ln\left( \dfrac{2.5}{3}\right)\) |
| \( 200k=\) | \(=\) | \(\ln\left( \dfrac{2.5}{3}\right)\) |
| \(k\) | \(=\) | \(\dfrac{1}{200}\ln\left( \dfrac{2.5}{3}\right)\) \(\,= -9.116\times 10^{-4}\) |
Exponential Decay
👉 New Data: $\,N_0=3,\;$ $k = -9.116\times 10^{-4}$
• How much of the radioactive substance would be left after 400 years?
| \(N\) | \(=\) | \(N_0e^{kt}\) |
| \(N\) | \(=\) | \(3e^{\left(-9.116\times 10^{-4}\right)(400)}\) |
| \(N\) | \(=\) | \(3e^{-0.36464}\) \(\approx 2.08334 \ldots \) |
| \(N\) | \(=\) | \(2.08\) grams |
After 400 years, it is predicted that there will be 2.08 grams remaining.
Exponential Decay
👉 New Data: $\,N_0=3,\;$ $k = -9.116\times 10^{-4}$
• What is the half-life of the radioactive substance?
| \(N\) | \(=\) | \(N_0e^{kt}\) |
| \(1.5\) | \(=\) | \(3e^{\left(-9.116\times 10^{-4}\right)t}\) |
| \(\dfrac{1.5}{3}\) | \(=\) | \(\dfrac{3e^{\left(-9.116\times 10^{-4}\right)t}}{3}\) |
| \(\dfrac{1.5}{3}\) | \(=\) | \(e^{\left(-9.116\times 10^{-4}\right)t}\) |
| \(\ln\left(1.5\over3\right)\) | \(=\) | \(\ln\left(e^{\left(-9.116\times 10^{-4}\right)t}\right)\) |
Exponential Decay
👉 New Data: $\,N_0=3,\;$ $k = -9.116\times 10^{-4}$
• What is the half-life of the radioactive substance?
| \(\ln\left(1.5\over3\right)\) | \(=\) | \(\ln\left(e^{\left(-9.116\times 10^{-4}\right)t}\right)\) |
| \(\ln\left(1.5\over3\right)\) | \(=\) | \(\left(-9.116\times 10^{-4}\right)t\) |
| \(\dfrac{\ln\left(1.5\over3\right)}{-9.116\times 10^{-4}}\) | \(=\) | \(\dfrac{\left(-9.116\times 10^{-4}\right)t}{-9.116\times 10^{-4}}\) |
| \(t\) | \(=\) | \(\dfrac{\ln\left(1.5\over3\right)}{-9.116\times 10^{-4}}\) \(= 760.36\) years |
The half-life of this radioactive substance is approx. 760 years.
Exponential Growth/Decay
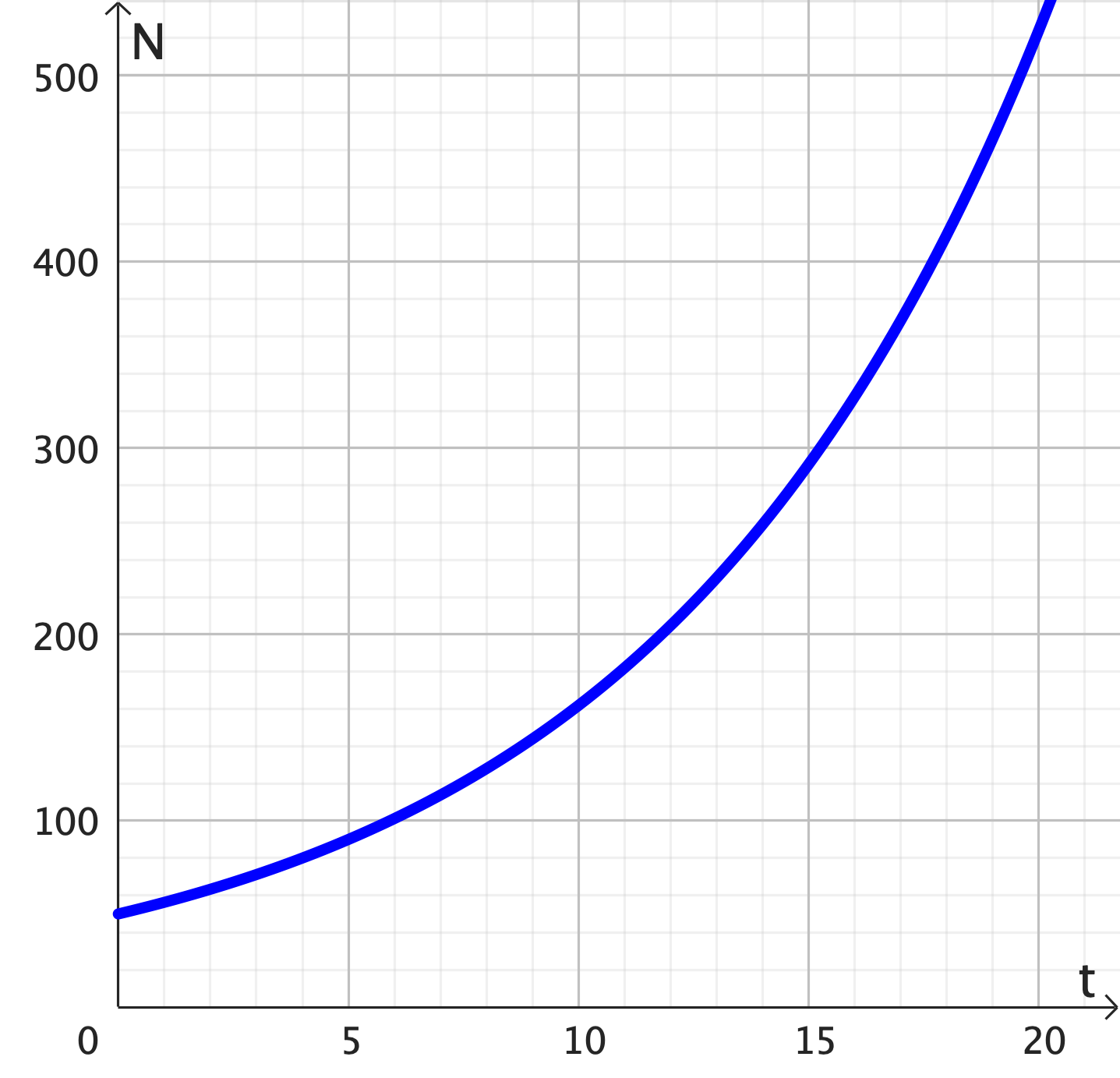
Growth ($k>0$) |
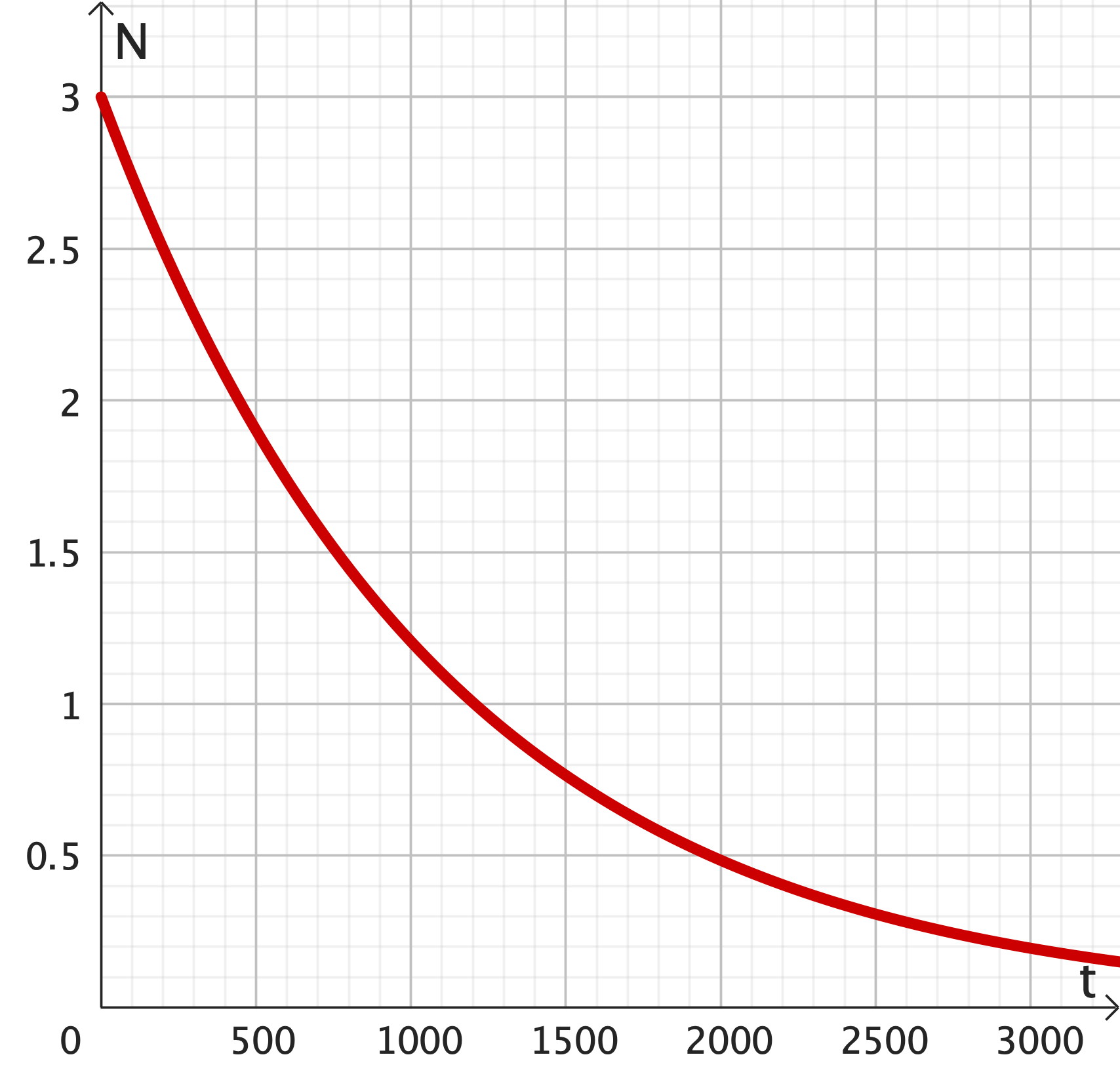
Decay ($k>0$) |
Solving Trigonometric Equations
Solve \(\,\sin (x) = \dfrac{1}{2}.\) Then \(x = 30^\circ \)
|
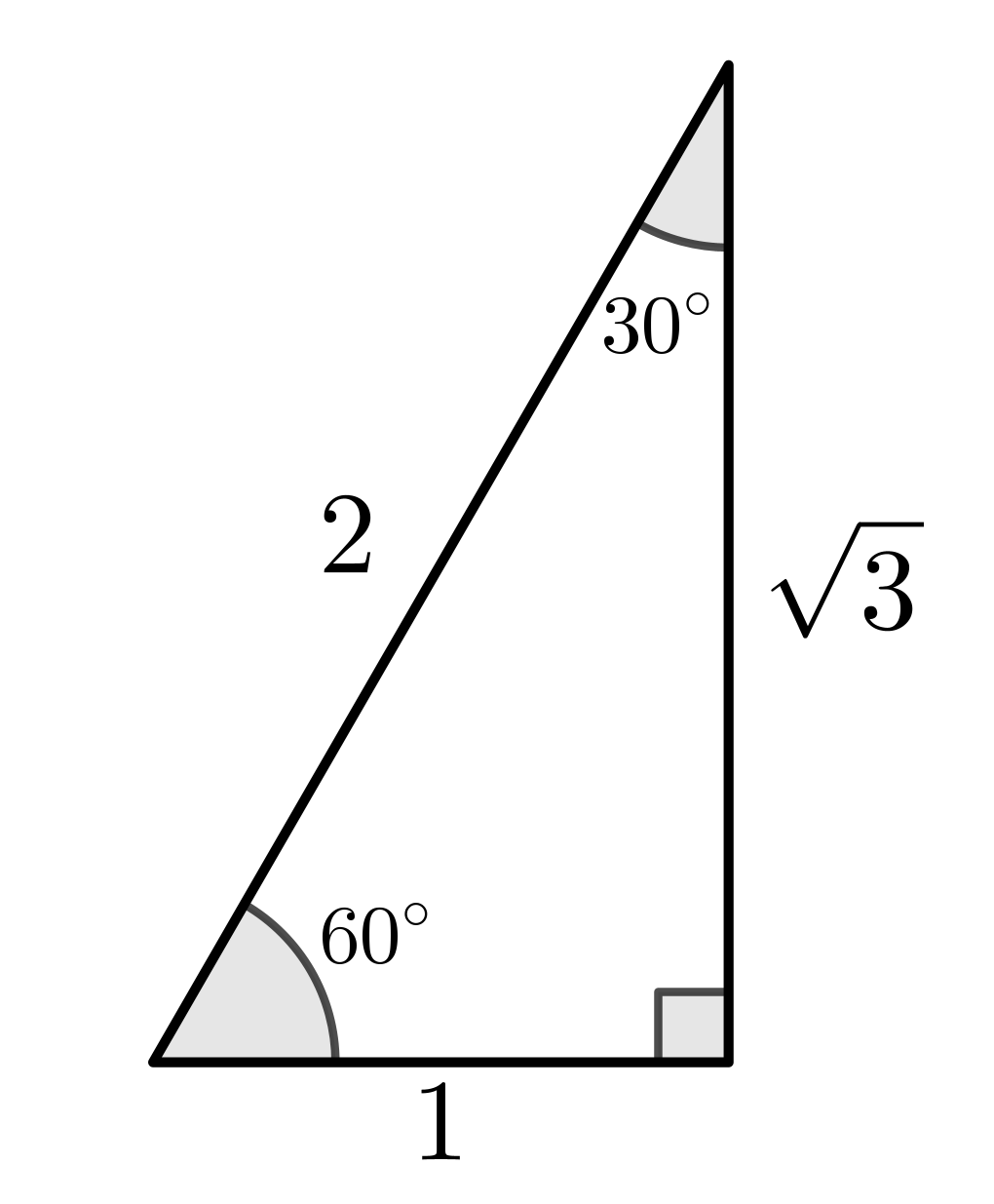
Solving Trigonometric Equations
Solve \(\,\sin (x) = \dfrac{1}{2}.\) Then \(x = 30^\circ \)
|
\(x = 30^\circ + 360^\circ\) \(=390^\circ \) \(x = 30^\circ + 2 \times360^\circ \) \( =750^\circ \) \(x = 30^\circ + 3 \times360^\circ \) \( =1080^\circ \) \(\qquad \qquad \vdots \) |
|
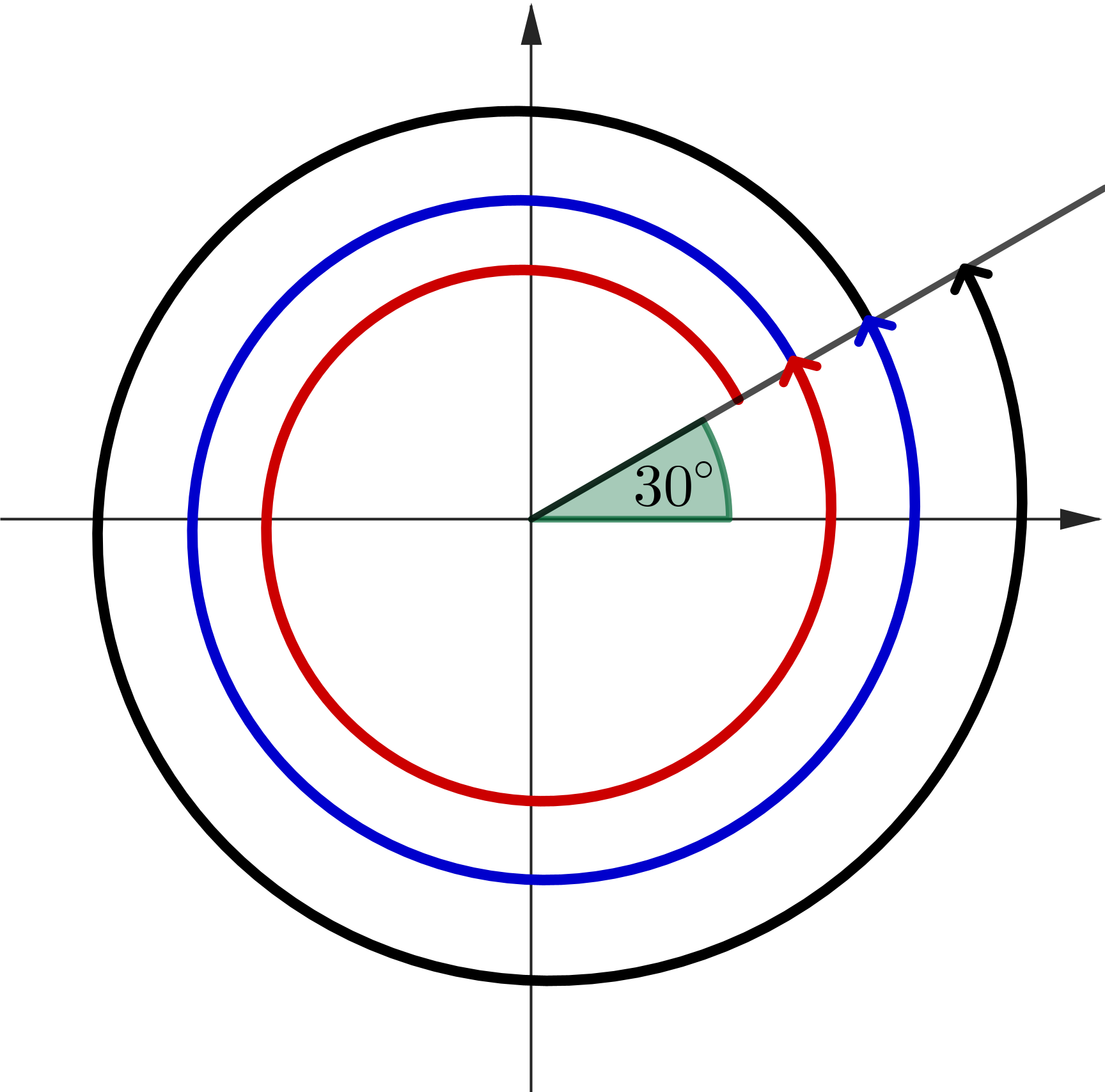
Solving Trigonometric Equations
Solve \(\,\sin (x) = \dfrac{1}{2}.\) Then \(x = 30^\circ \)
|
\(x = \dfrac{\pi}{6} + 2\pi\) \(=\dfrac{13\pi}{6} \)
\(x = \dfrac{\pi}{6} + 2 \times 2\pi \)
\(x = \dfrac{\pi}{6} + 3 \times 2\pi \) \( =\dfrac{37\pi}{6} \) \(\qquad \qquad \vdots \) |
|
Solving Trigonometric Equations
Solve \(\,\sin (x) = \dfrac{1}{2}.\) Then \(x = -330^\circ \)
|
\(x = -330^\circ\) \(x = -330^\circ - 360^\circ \) \( \;\;\, =-690^\circ \) \(x = -330^\circ + 2 \times360^\circ \) \(\;\;\, =-1050^\circ \) \( \quad \vdots \) |
Solving Trigonometric Equations
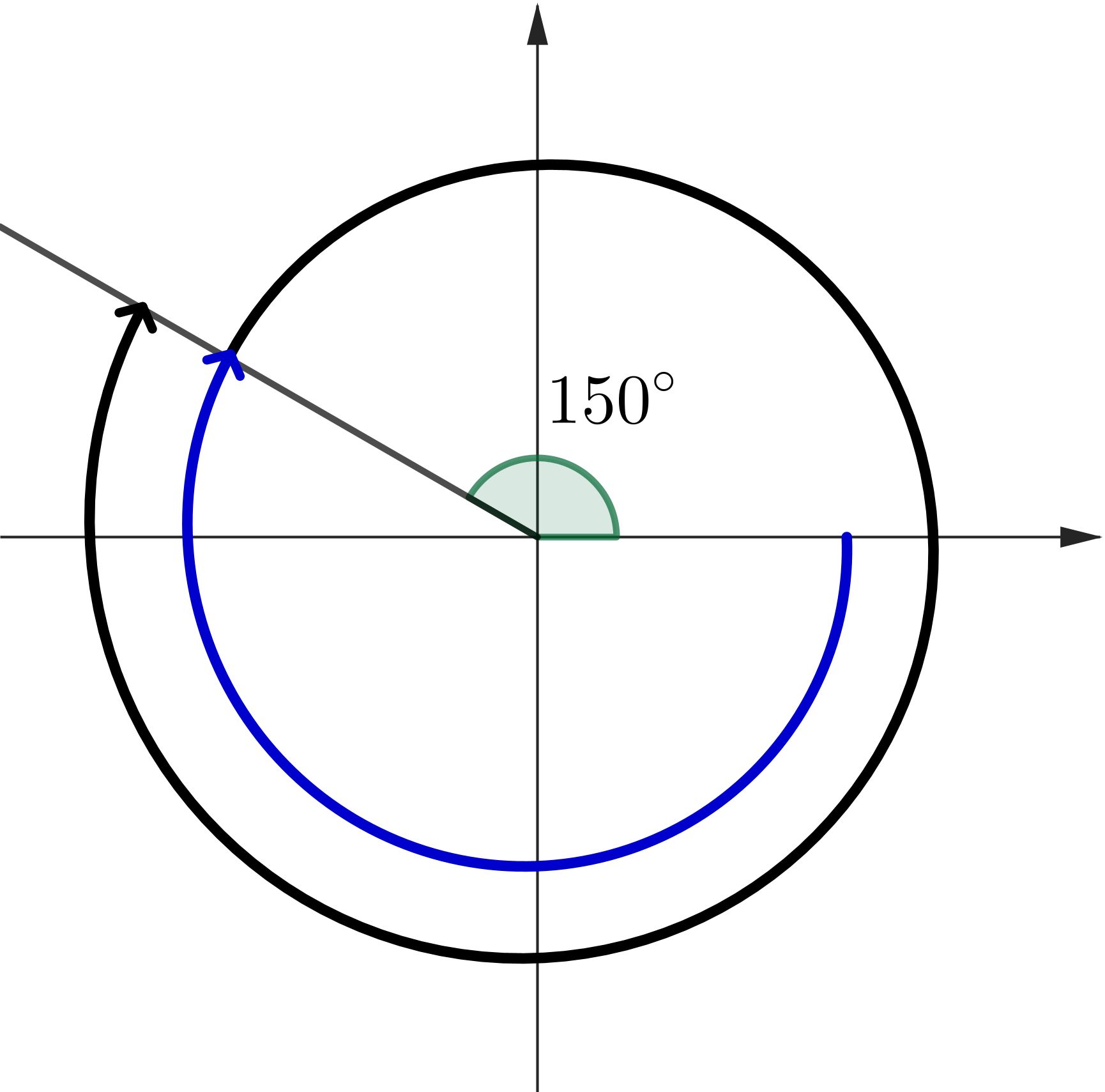
Solve \(\,\sin (x) = \dfrac{1}{2}.\) Then \(x = 150^\circ \)
|
\(x = 150^\circ\) \(x = 150^\circ + 360^\circ \) \( =510^\circ \) \(x = -210^\circ \) \(x = -210^\circ - 360^\circ \) \( =-570^\circ \) |
|
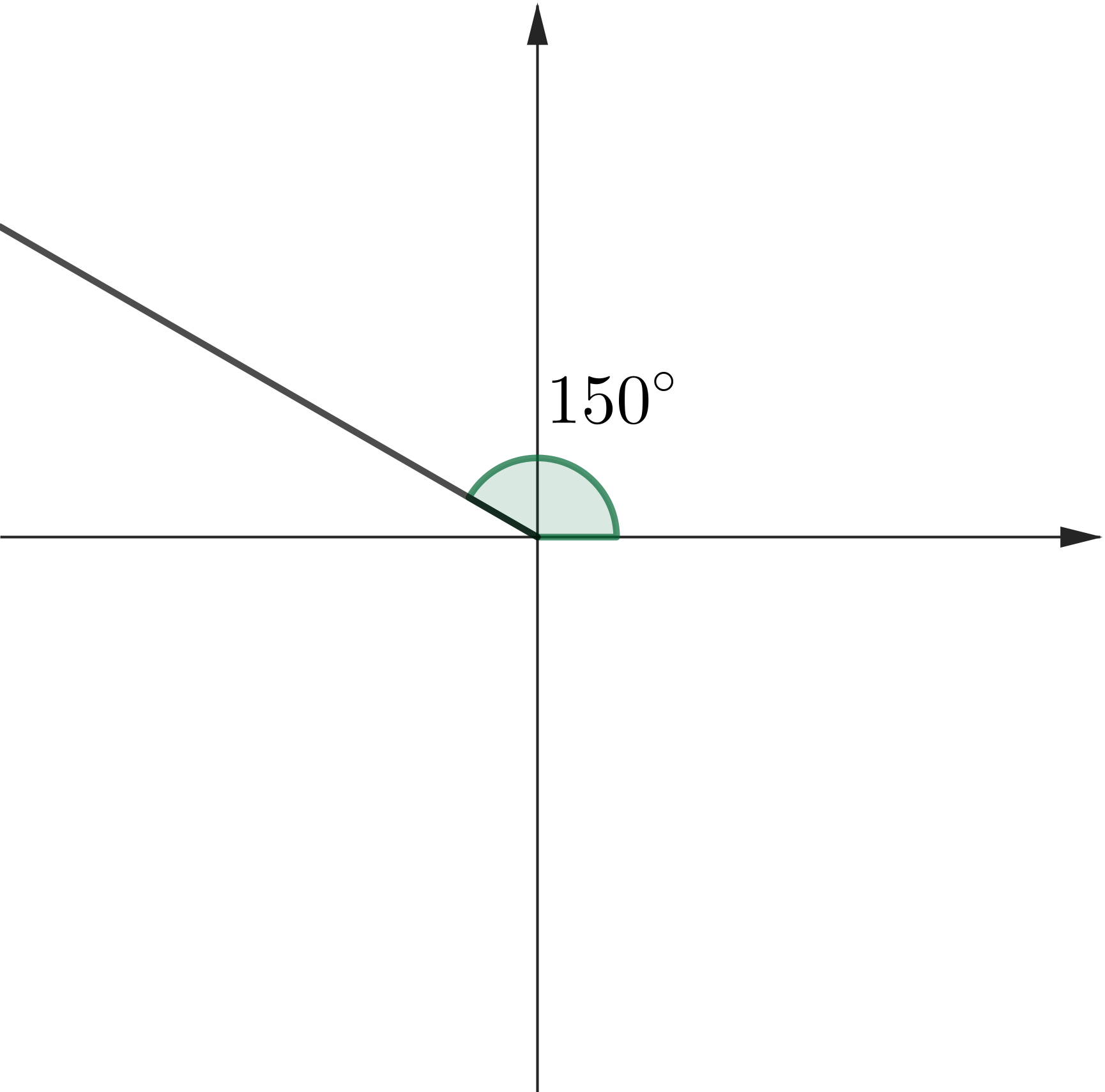
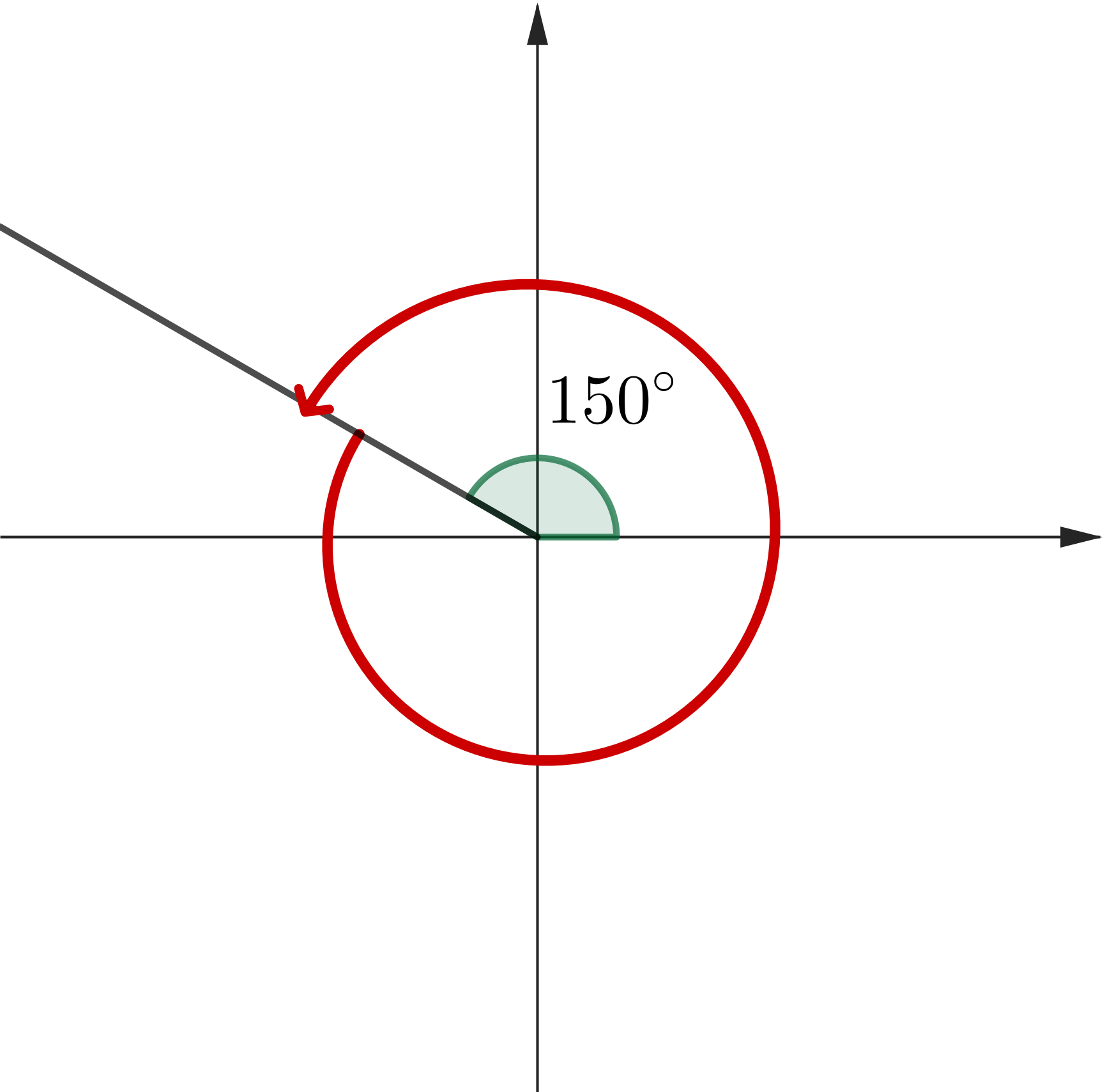
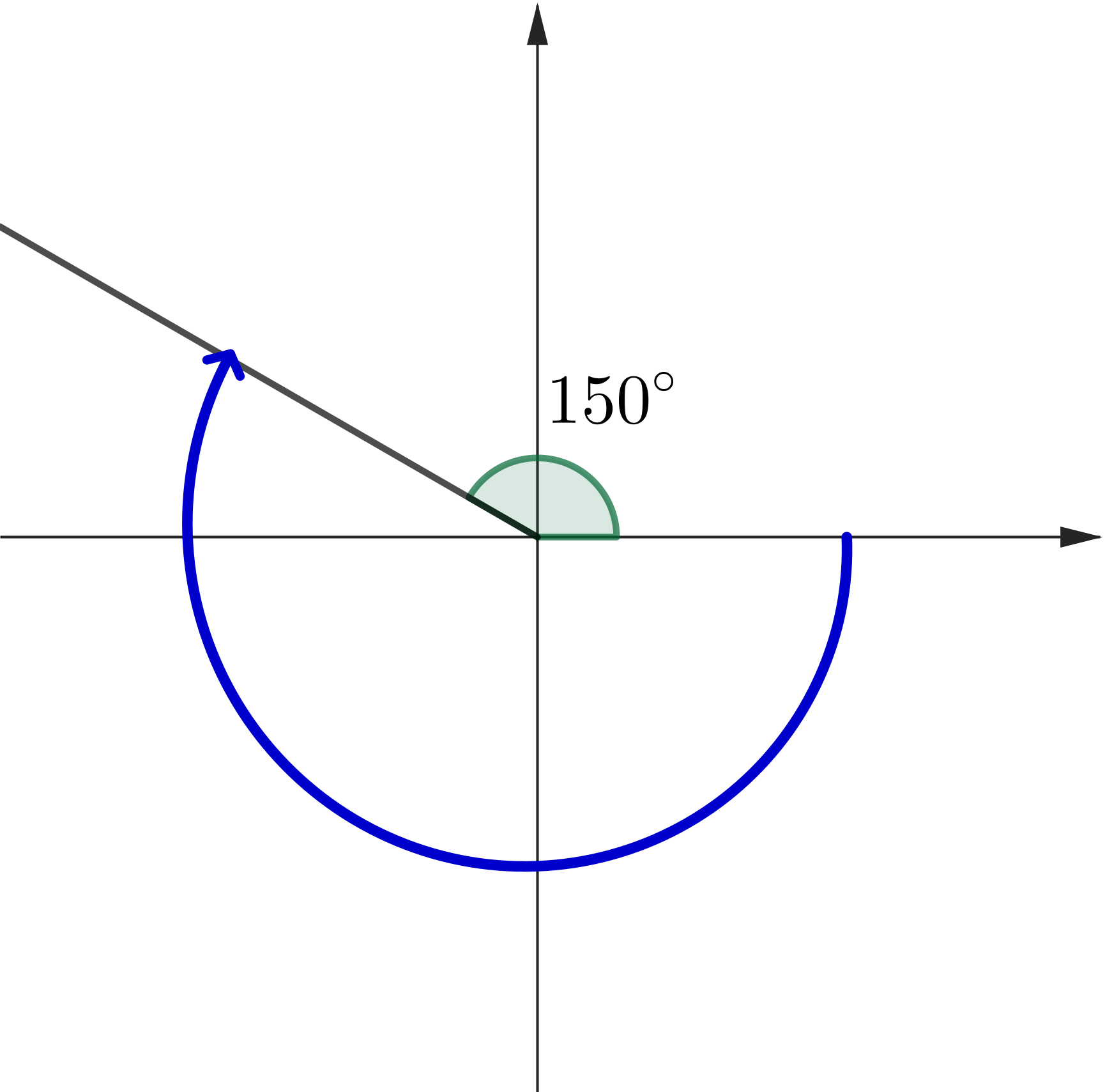
Solving Trigonometric Equations
So, what is the solution of $\sin \left(x\right)=\dfrac{1}{2}$?
Do we need to write an $\infty$ list of values of $x$?
Solving Trigonometric Equations
Solve $\sin (x) =\dfrac{1}{2},\,$ where $\,0^\circ \leq x \leq 360^\circ$
• $x = 30^\circ$
• $x = 150^\circ$
Is $x = 210^\circ$ a solution? 🤔
Answer: No, because $\sin\left(210^\circ\right)=-\dfrac{1}{2}$
Solving Trigonometric Equations
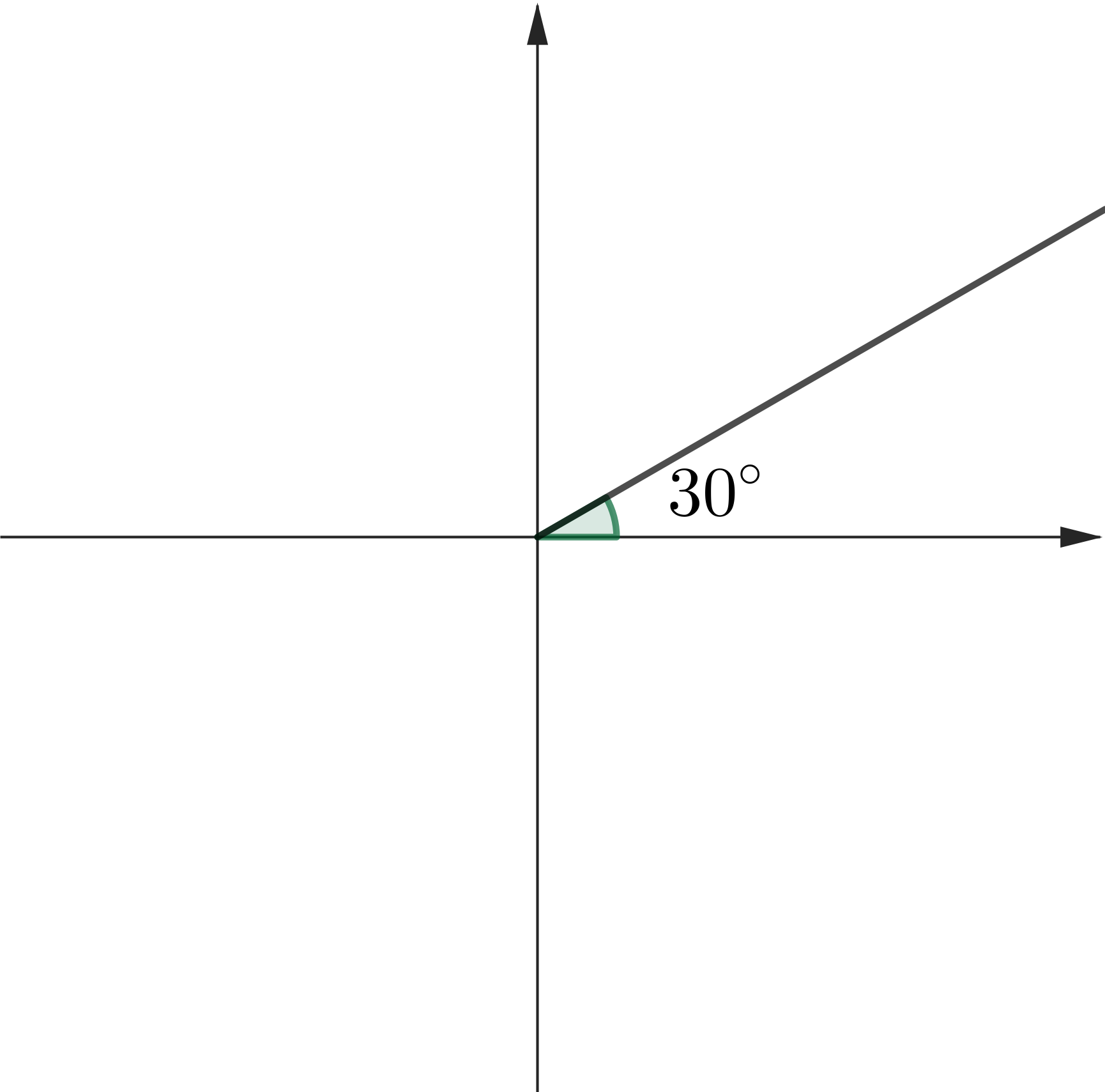
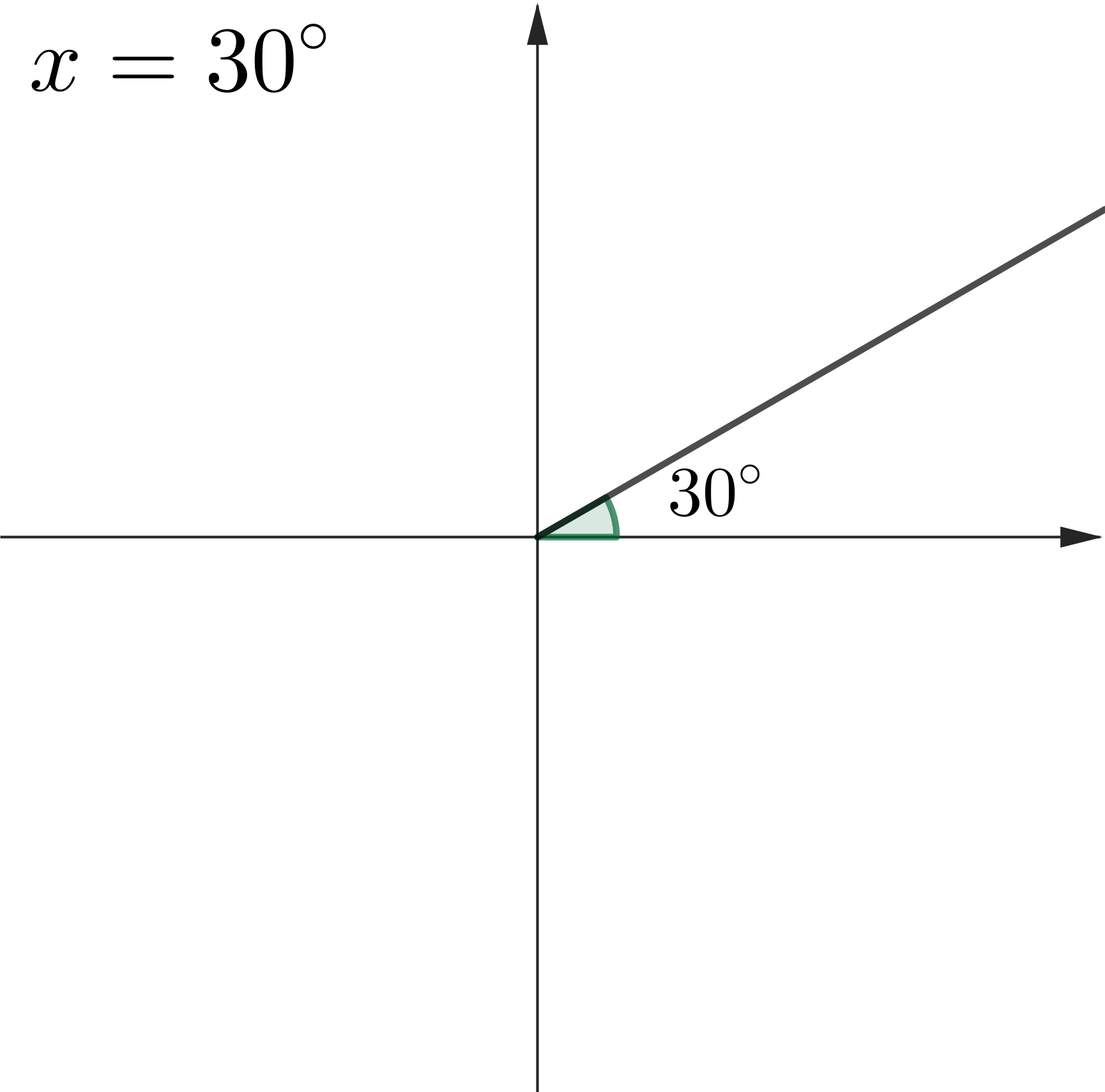
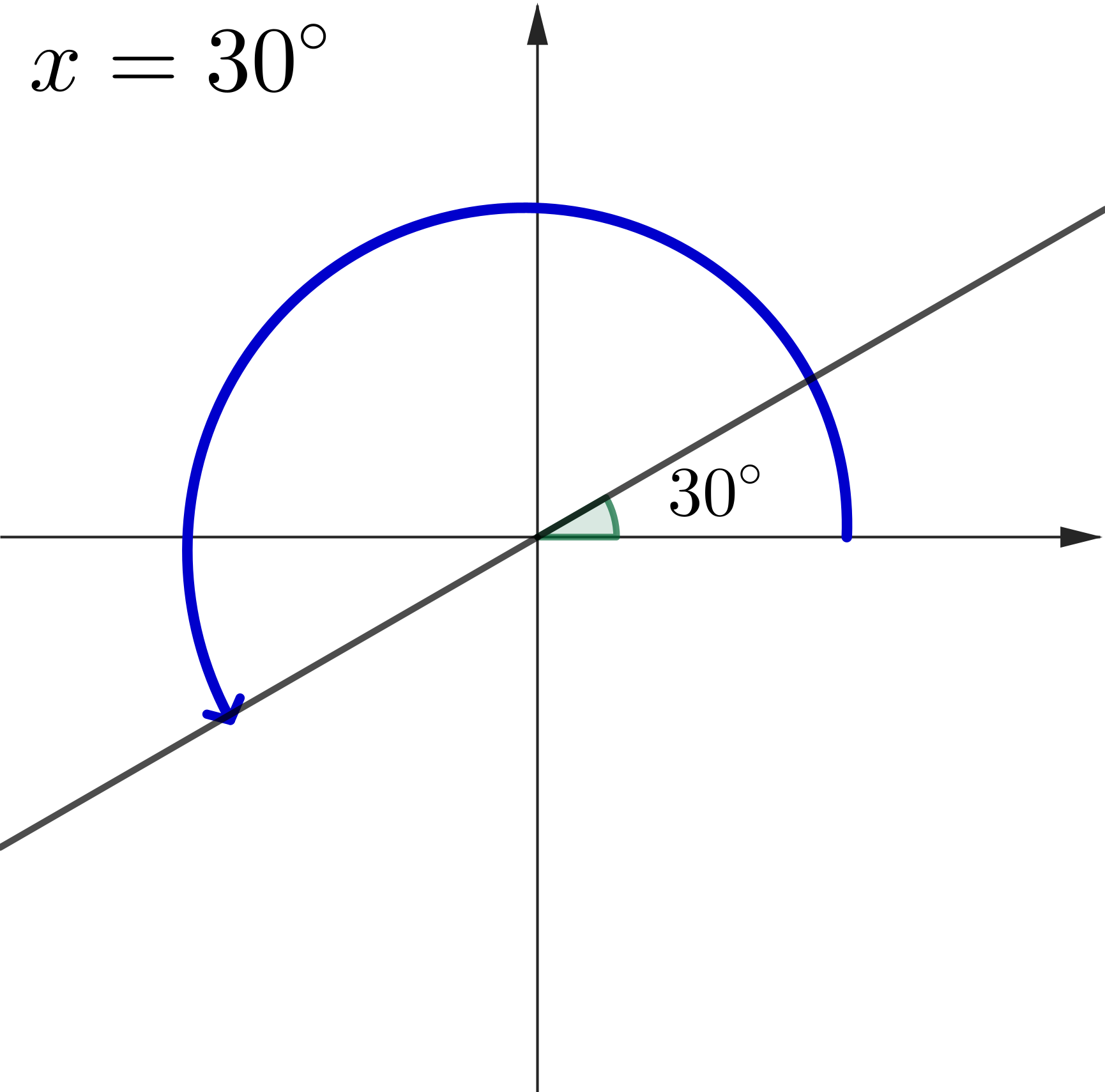
Example 1: Solve $\tan (x) =\dfrac{1}{\sqrt{3}},\,$ where $\,0^\circ \leq x \leq 360^\circ$
|
|
|
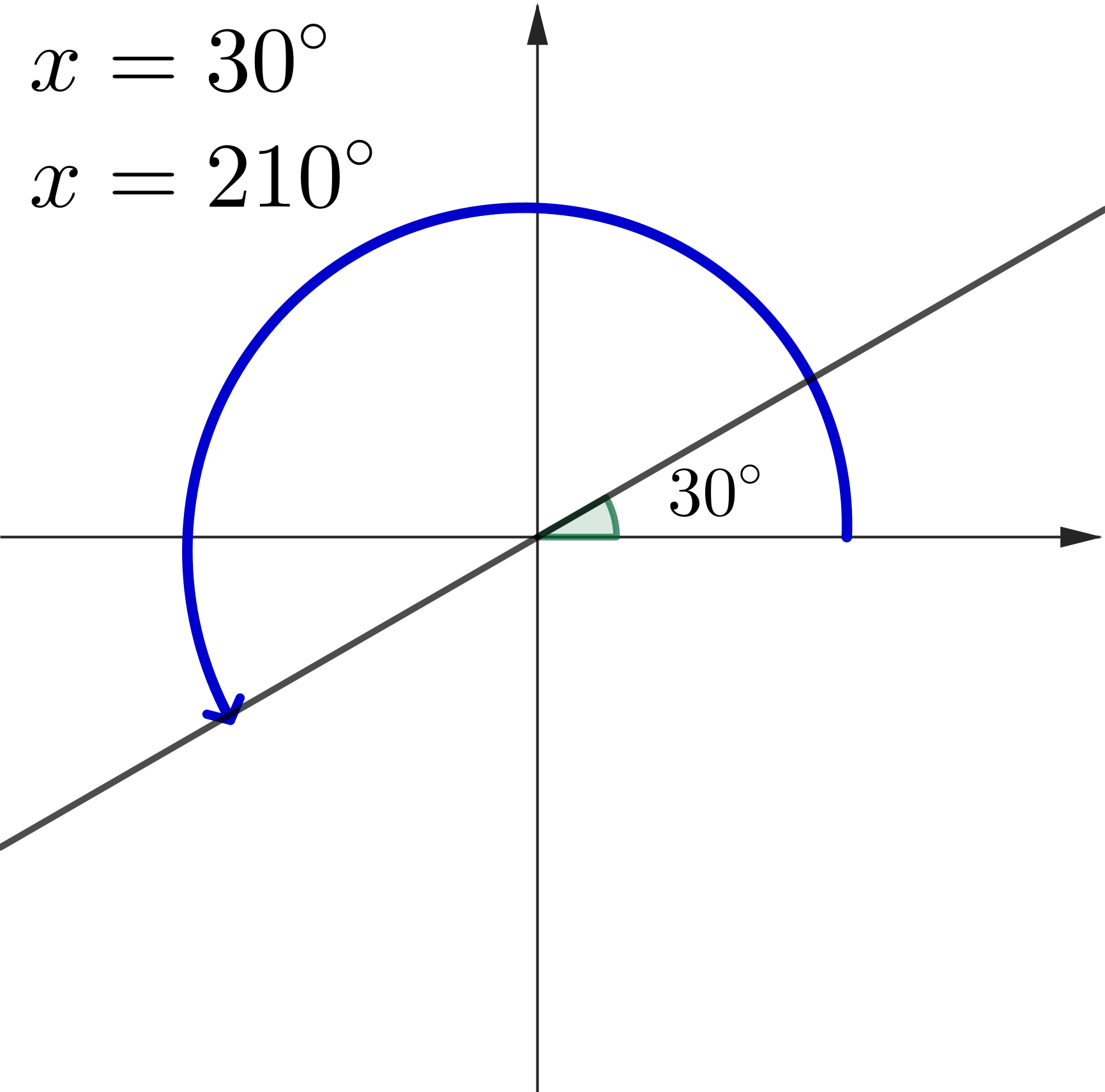
Solving Trigonometric Equations
Example 2: Solve $\cos (x) =\dfrac{1}{\sqrt{2}},\,$ where $\,0^\circ \leq x \leq 360^\circ$
|
|
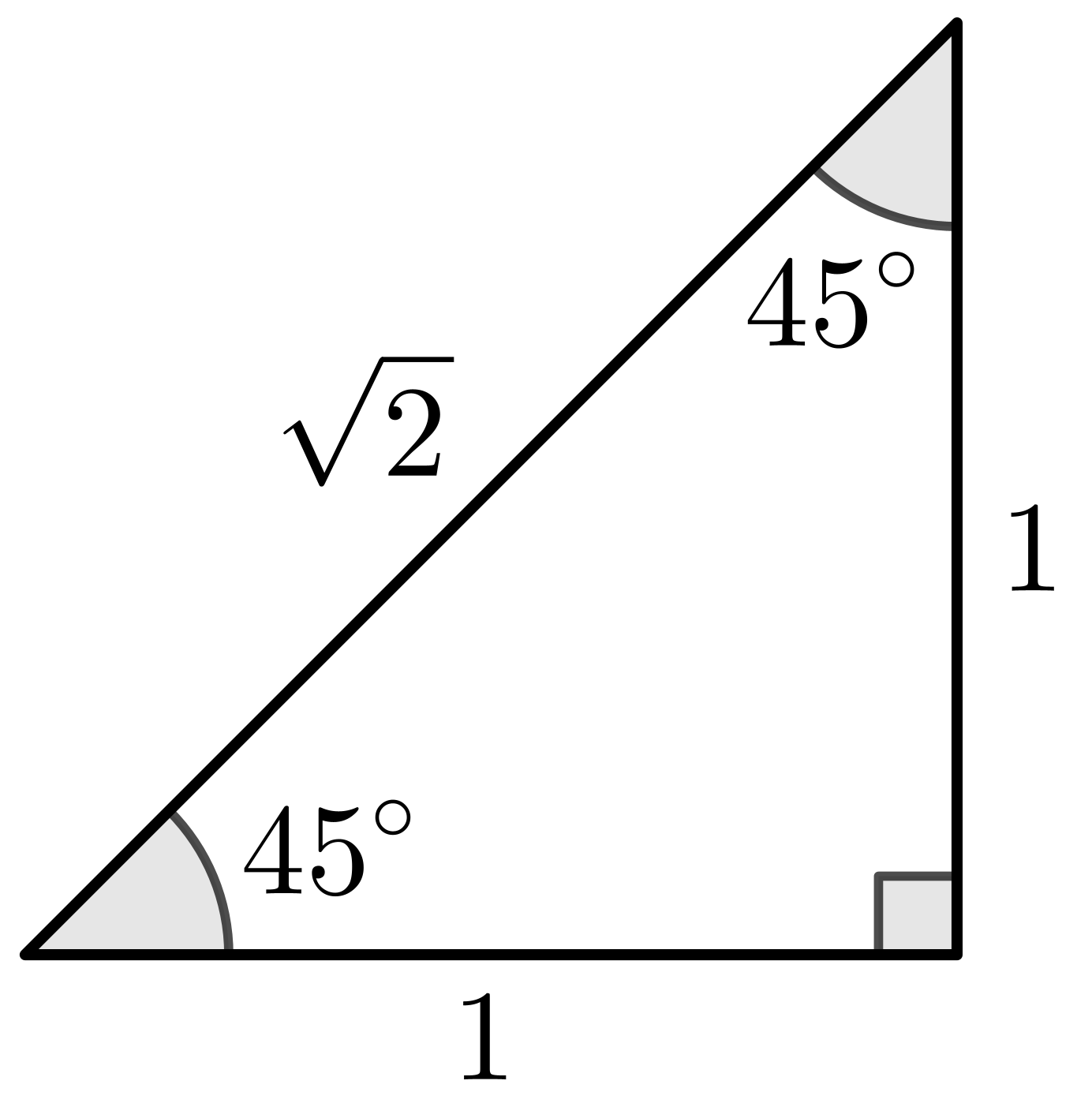
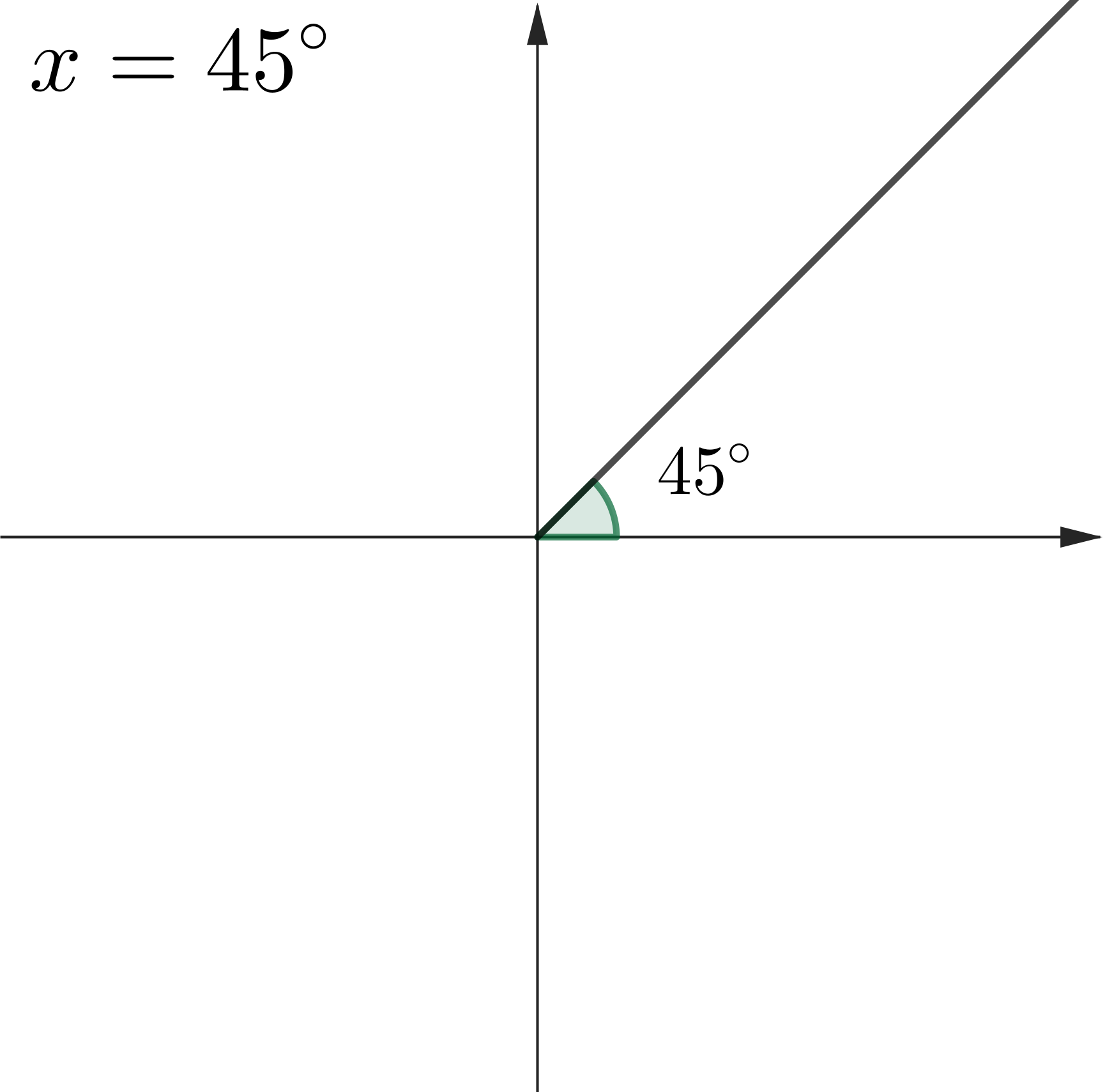
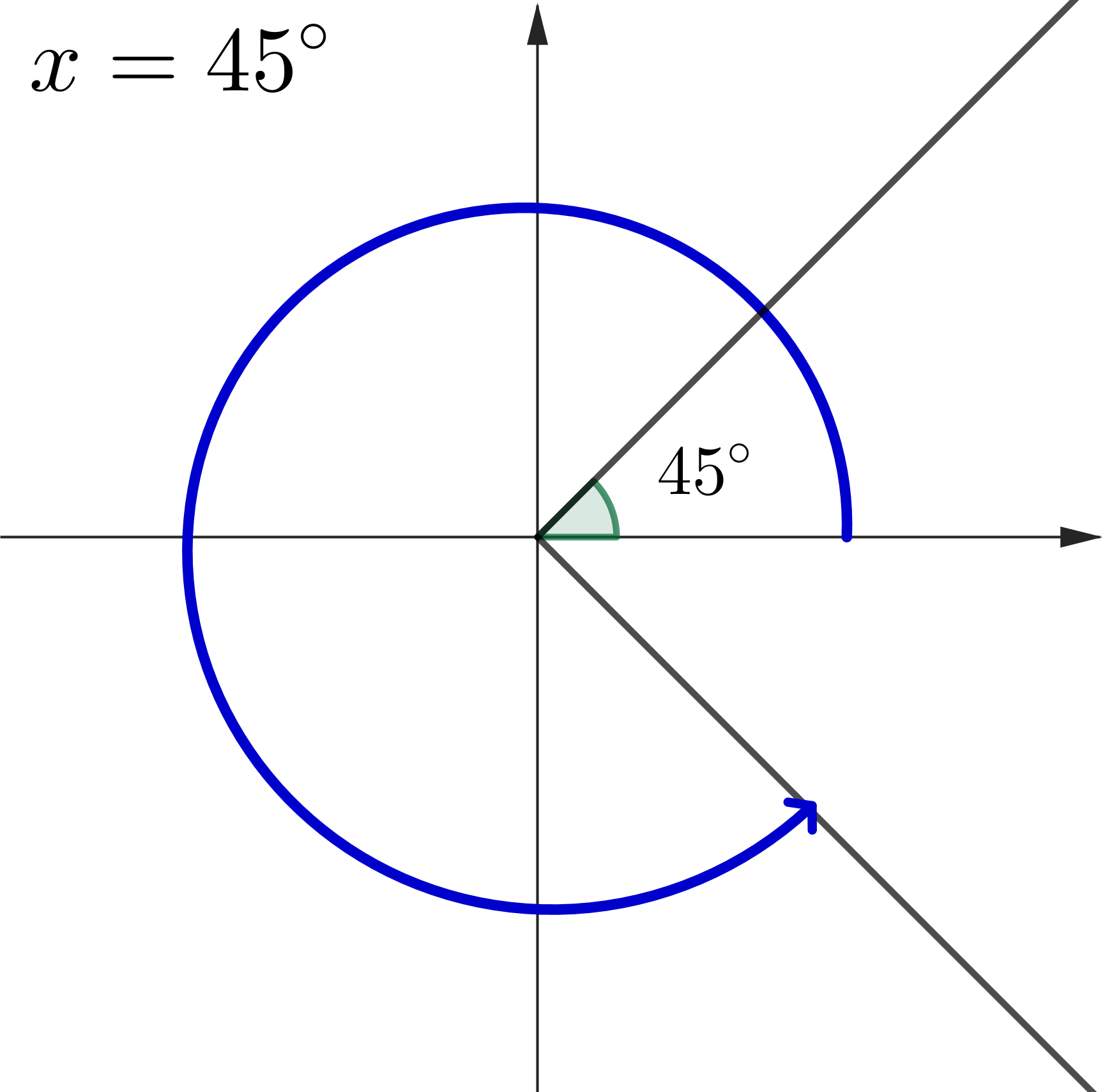
Solving Trigonometric Equations
Example 3: Solve $\sin (x) =-\dfrac{\sqrt{3}}{2},\,$ where $\,0^\circ \leq x \leq 360^\circ$
👉 First solve $\sin (y) =\dfrac{\sqrt{3}}{2}$
|
|
|
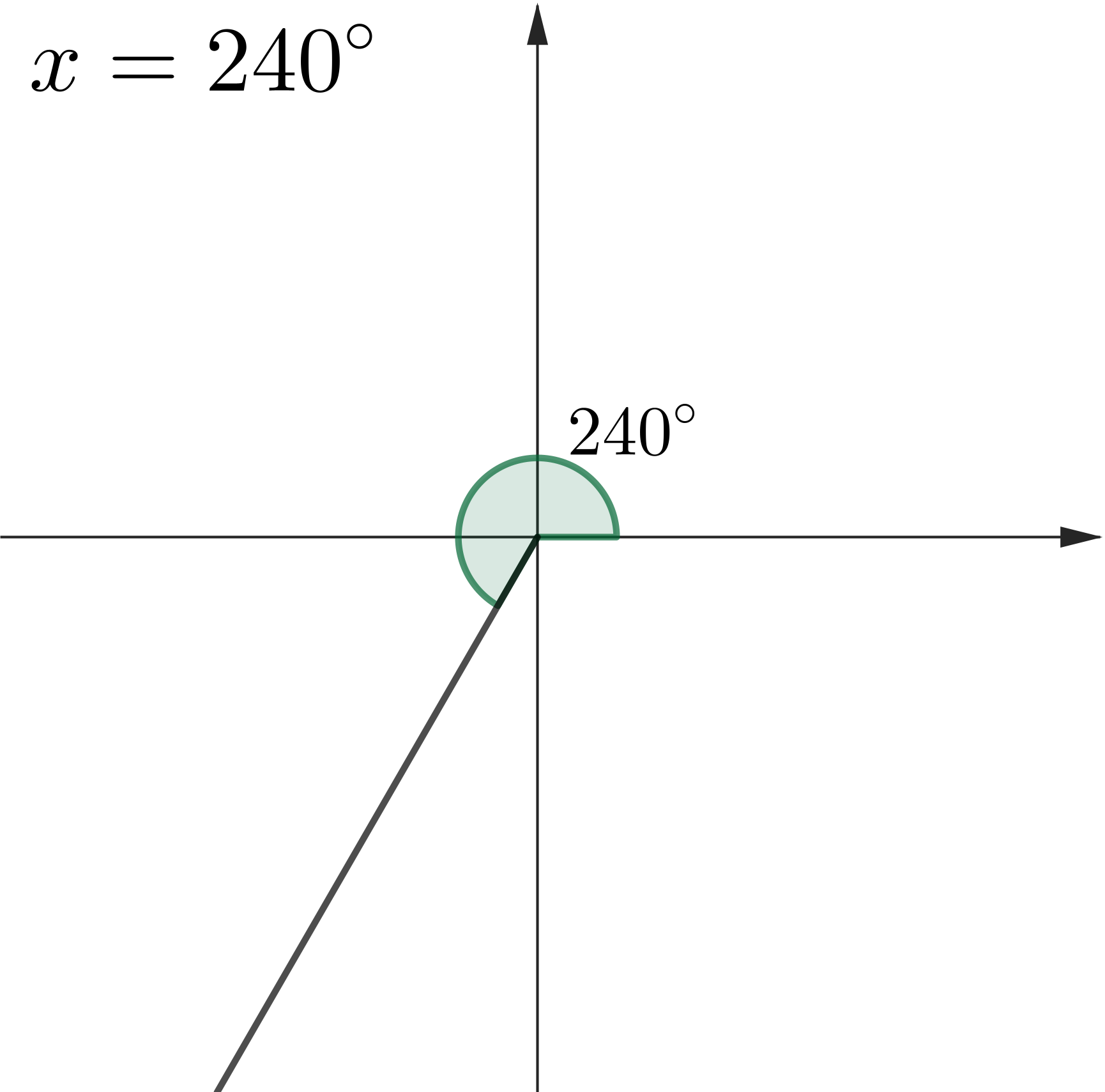
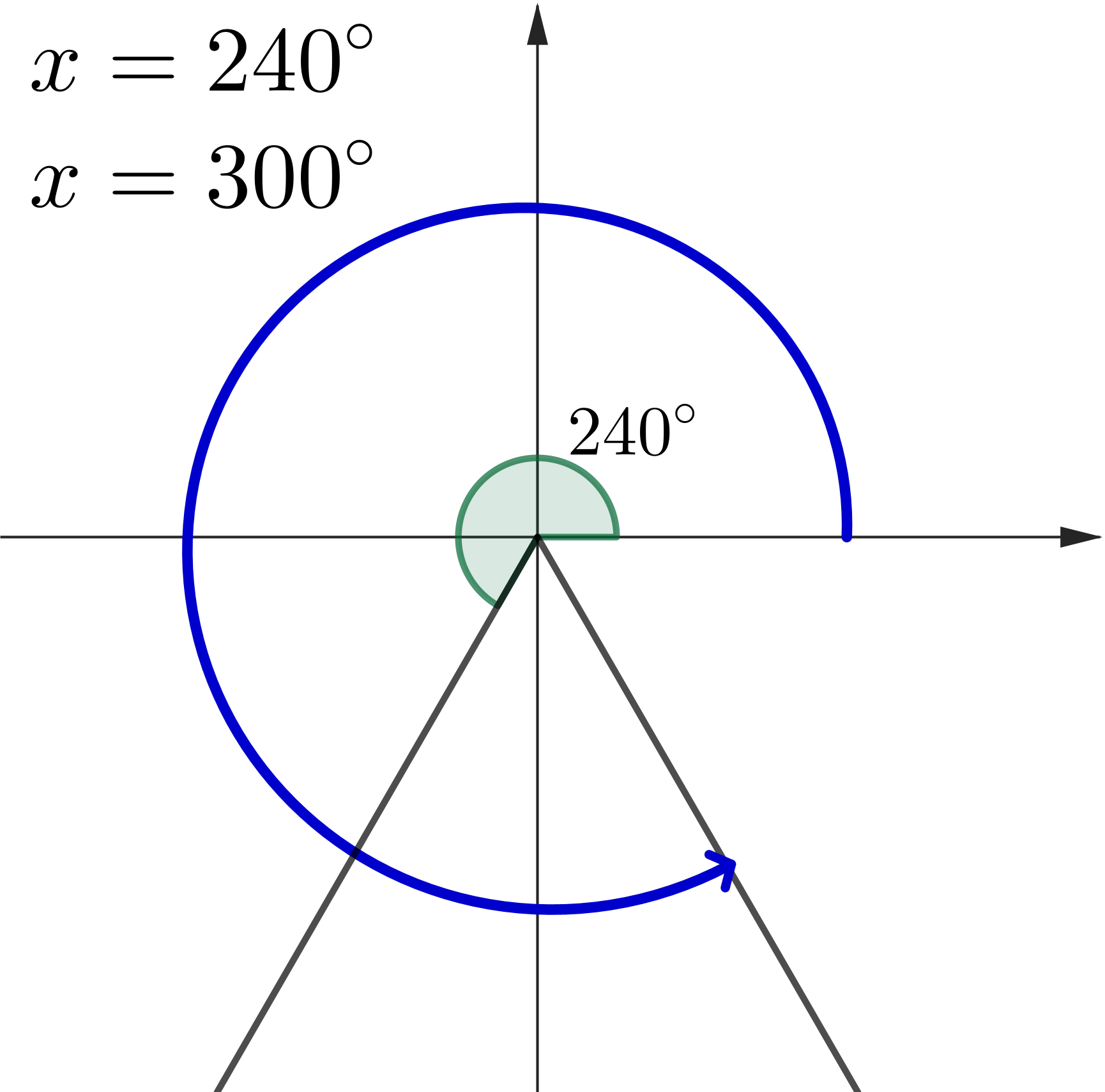
Introduction to Functions
What is a function? 🤔
Introduction to Functions
Introduction to Functions
What is a function? 🤔
A function is a rule that associates a unique output to each input.
Definition: A function assigns to each element of $X$ (set of numbers) exactly one element of $Y$ (also a set of numbers).
The set $X$ is called the domain of the function and the set $Y$ is called the range of the function.
Introduction to Functions
$f(x) = 3x+2$
|
$f(3) = 3(3)+2$ $\quad\;\;\,\, =9 + 2$ $\quad\;\;\,\, =11$ |
$f(5) = 3(-5)+2$ $\quad\;\;\,\, = -15+2$ $\quad\;\;\,\, = -13$ |
Introduction to Functions
$f(x) = x^2+3$
|
$f(2) = (2)^2+3$ $\quad\;\;\,\, =4 + 3$ $\quad\;\;\,\, =7$ |
$f(-1) = (-1)^2+3$ $\qquad\;\, = 1+3$ $\qquad\;\, = 4$ |
Introduction to Functions
$f(x) = x^2-2x+4$
|
$f(-4) = (-4)^2-2(-4)+4$ $\qquad\,\, =16 + 8+4$ $\qquad\,\,=28$ |
$f(2a) = (2a)^2-2(2a)+4$ $\qquad\,\,= 4a^2-4a+4$
|
Introduction to Functions
|
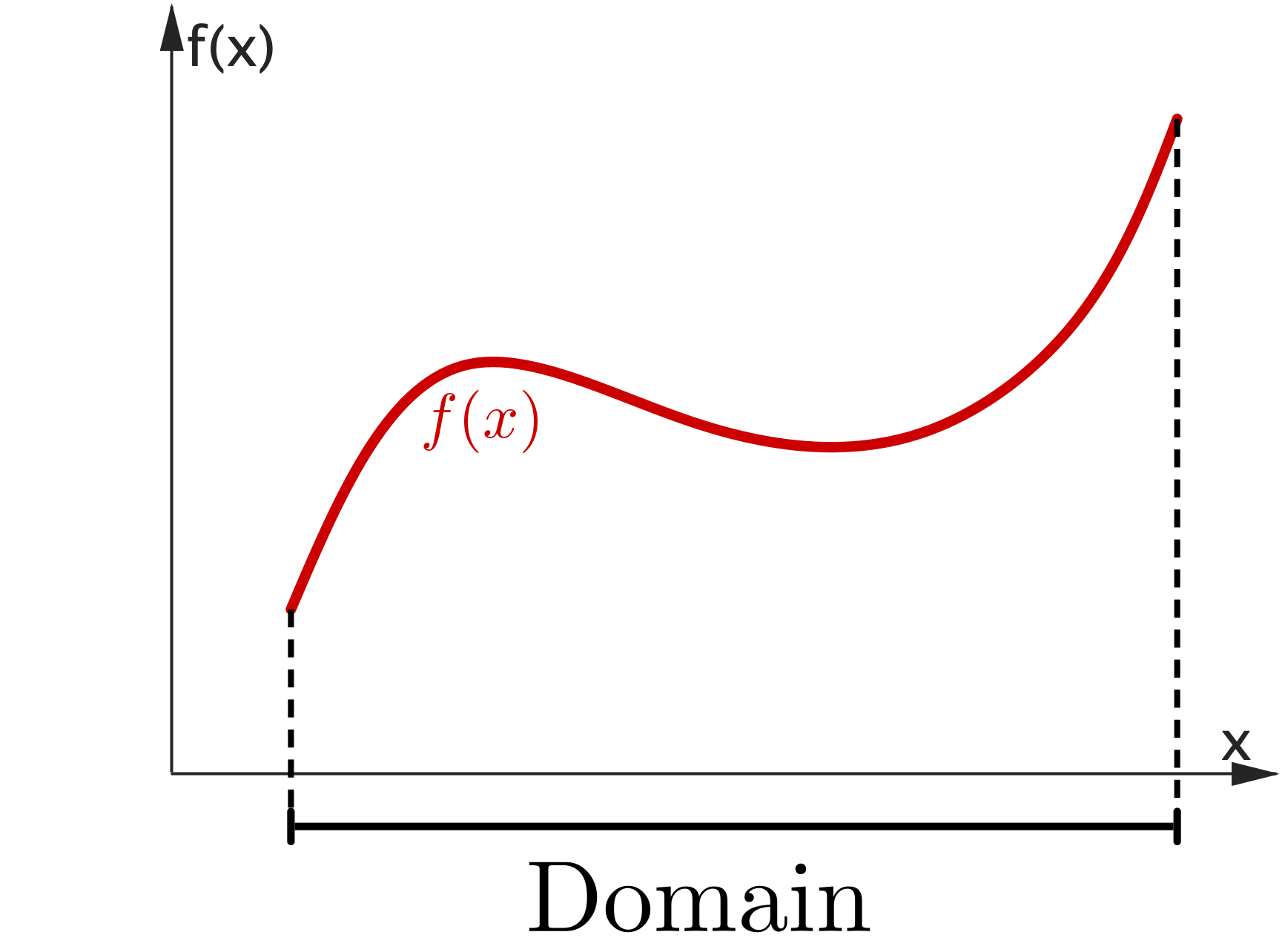
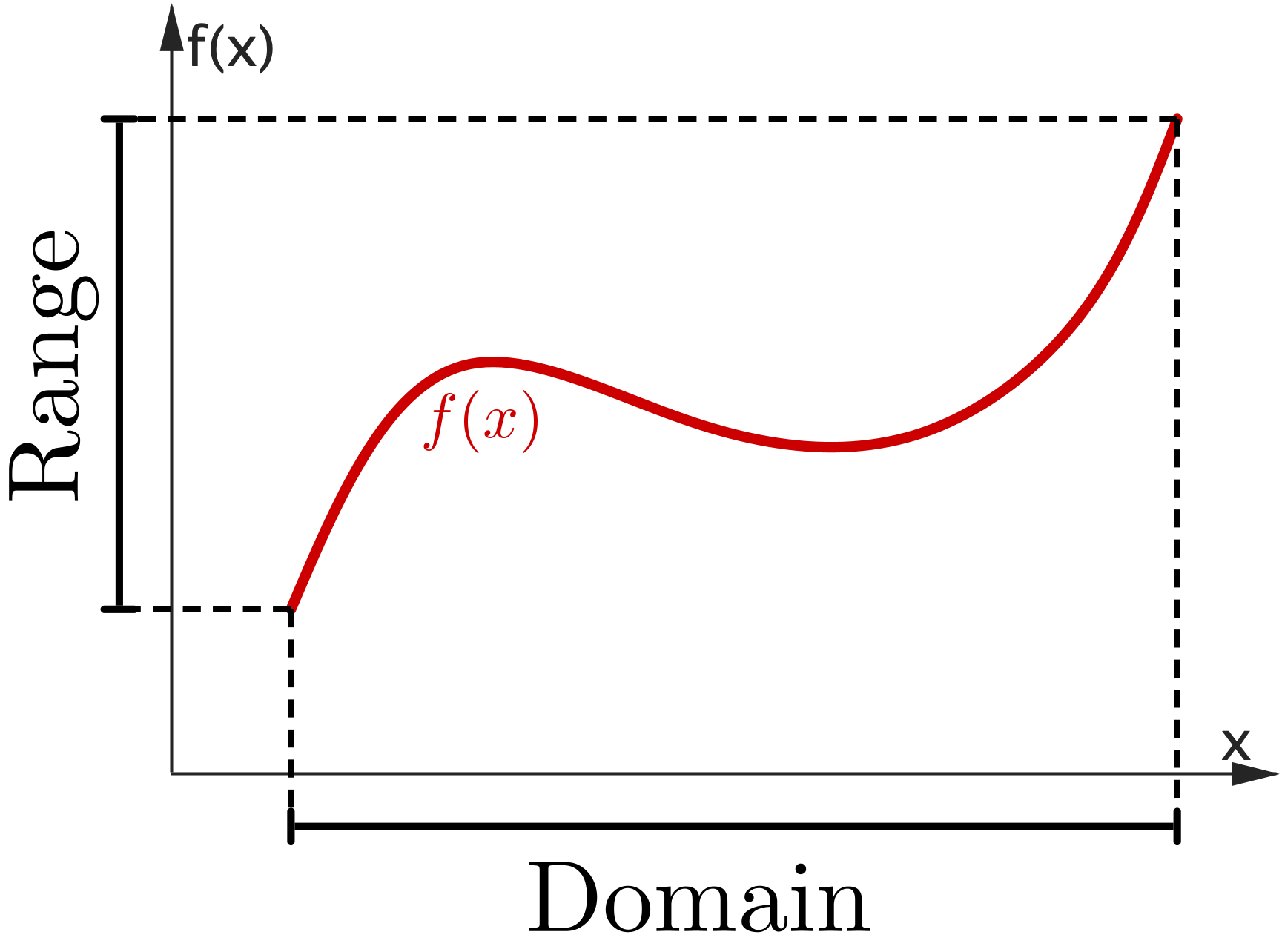
The domain of $f(x)$ is the set of all possible values of $x$ for which the function is defined (i.e. all the values of $x$ that can be used with the function). The range of $f (x)$ is the set of all possible values that can be returned by the function. |
Introduction to Functions
Consider the function $f(x)= \sqrt{x}$
|
$f(0) = 0$ $f(2) = \sqrt{2}$ $f(9) = \sqrt{9}$ $f(-4) = \sqrt{-16}$ Not valid! Domain: All positive values of $x,$ including $x=0.$ Domain: $x\geq 0.\qquad \qquad\;\;$ Range: $f(x)\geq 0 .$ |
Introduction to Functions
Consider the function $f(x)= \dfrac{1}{x-5}$
|
$f(0) = \dfrac{1}{(0)-5}$ $=-\dfrac{1}{5}$ $f(-2) = \dfrac{1}{(-2)-5}$ $=-\dfrac{1}{7}$ $f(9) = \dfrac{1}{(9)-5}$ $=\dfrac{1}{4}$ $f(5) = \,$ Not possible! 1/0! Domain: All real values of $x,$ except $x=5.$ Range: All real values except $0.$ |
Mathematical art with basic functions
$f(x) = \sqrt{6^2-x^2},\,$ $g(x) = 2 + 2 \sin(\text{floor}(x-t) 4321),\,$ $h_k(x) = \dfrac{-5}{k}+\dfrac{2}{5}, \,$ $k=0,1,\ldots,10$