
Foundation Mathematics
1017SCG
Week 10
Topics
- Definition of the Derivative (first principles)
- Tables of Derivatives
- Applications of Derivatives (Turning points, Greatest and Least values, Tangent lines)
Definition of the Derivative (first principles)
Definition of the Derivative (first principles)
Definition of the Derivative (first principles)
What is the gradient of any possible function? 🤔
Definition of the Derivative (first principles)
Definition of the Derivative (first principles)
|
|
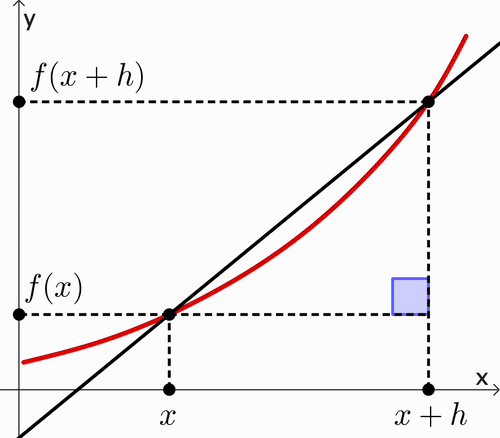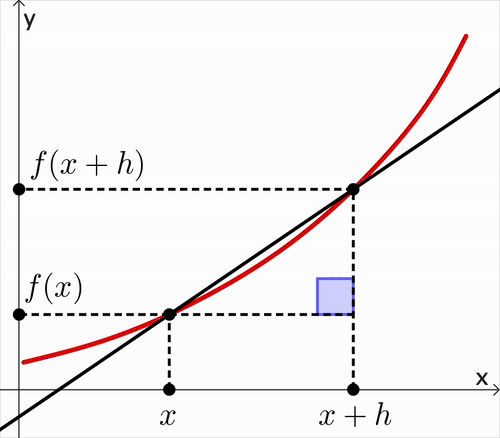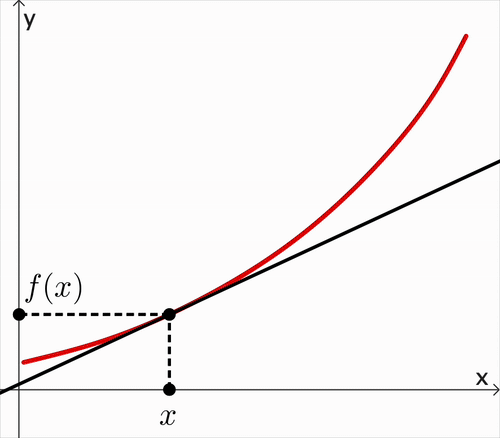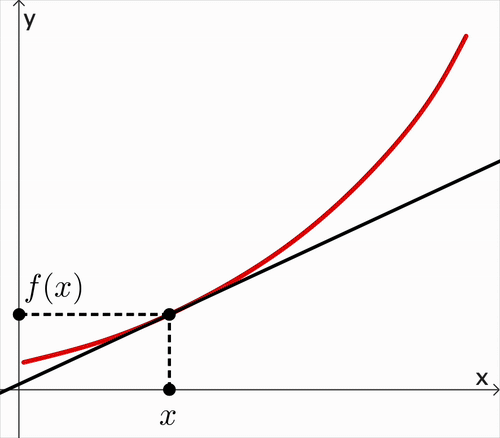
Average Gradient $\quad= \dfrac{f(x+h)-f(x)}{h}$ |
Definition of the Derivative (first principles)
|
Average Gradient $\quad= \dfrac{f(x+h)-f(x)}{h}$ Gradient of the curve $=\ds\lim_{h\ra 0} \dfrac{f(x+h)-f(x)}{h}$ |
Definition of the Derivative (first principles)
Gradient of a curve $\,\ra\,$ Slope of the tangent line
We call it the instantaneous rate of change.
The Derivative of the function $y=f(x)$ is given by:
$\dfrac{dy}{dx}=$ $\ds \lim_{h\ra 0} \frac{f(x+h)-f(x)}{h}$
Example 1
Compute the derivative of $y = 3x + 7$ using first principles.
Write $\,f(x)= 3x+ 7 .$ Then
$f(x+h)$ $=3(x+h) + 7$ $=3x + 3h + 7$
Thus
$\dfrac{f(x+h)-f(x)}{h}$ $=\dfrac{(3x+3h+7) -(3x+7)}{h}$ $=\dfrac{3h}{h}$ $=3$
Hence $\;\ds\frac{dy}{dx}= \lim_{h\ra 0}\dfrac{f(x+h)-f(x)}{h}$ $=\ds \lim_{h\ra 0} 3$ $=3$
Example 2
Compute the derivative of $y = x^2$ using first principles.
Write $\,f(x)= x^2.$ Then
$f(x+h)$ $=(x+h)^2$ $=x^2 + 2xh + h^2$
Thus
$\;\; \dfrac{f(x+h)-f(x)}{h}$ $=\dfrac{\left(x^2 + 2xh + h^2\right) -\left(x^2\right)}{h}$
$\qquad \qquad \qquad \;\;\;\, =\dfrac{ 2xh + h^2}{h}$ $=\dfrac{ \left(2x + h\right)h}{h}$ $=2x + h$
Example 2
Compute the derivative of $y = x^2$ using first principles.
Write $\,f(x)= x^2.$ Then
👉 $\;\;\dfrac{f(x+h)-f(x)}{h}$ $=2x + h$
Hence
$\;\ds \frac{dy}{dx} = \lim_{h\ra 0}\dfrac{f(x+h)-f(x)}{h}$ $=\ds \lim_{h\ra 0} (2x + h)$ $=2x$

Big question
Can we always compute the derivative of any function $f(x)$ by computing the limit \[ \ds \lim_{h\ra 0}\frac{f(x+h)-f(x)}{h}? \]


Consider $\;y=x^3$
|
\( \begin{align*} \frac{dy}{dx} &= \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \qquad\qquad\qquad \end{align*} \) \( \begin{align*} &= \lim_{h \to 0} \frac{(x+h)^3 - x^3}{h} \\ &= \lim_{h \to 0} \frac{x^3 + 3x^2h + 3xh^2 + h^3 - x^3}{h} \\ &= \lim_{h \to 0} \frac{3x^2h + 3xh^2 + h^3}{h} \\ &= \lim_{h \to 0} \left( 3x^2 + 3xh + h^2 \right) \\ &= 3x^2 \end{align*} \) |

|
Now consider $\;y = x^4 - x^3 + 2x^2 - 1$
|
\( \begin{align*} \frac{dy}{dx} &= \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \end{align*} \) \( \begin{align*} &= \lim_{h \to 0} \frac{(x+h)^4 - (x+h)^3 + 2(x+h)^2 - 1 \;-\; (x^4 - x^3 + 2x^2 - 1)}{h} \\ &= \lim_{h \to 0} \frac{(x^4 + 4x^3h + 6x^2h^2 + 4xh^3 + h^4) - (x^3 + 3x^2h + 3xh^2 + h^3)}{h} \\ &\quad \quad \quad + \frac{(2x^2 + 4xh + 2h^2) - 1 - (x^4 - x^3 + 2x^2 - 1)}{h} \\ &= \lim_{h \to 0} \frac{x^4 + 4x^3h + 6x^2h^2 + 4xh^3 + h^4 - x^3 - 3x^2h - 3xh^2 - h^3}{h} \\ &\quad\quad \quad + \frac{2x^2 + 4xh + 2h^2 - 1 - x^4 + x^3 - 2x^2 + 1}{h} \\ &= \lim_{h \to 0} \frac{4x^3h + 6x^2h^2 + 4xh^3 + h^4 - 3x^2h - 3xh^2 - h^3 + 4xh + 2h^2}{h} \\ &= \lim_{h \to 0} \frac{4x^3h - 3x^2h + (6x^2h^2 - 3xh^2 + 2h^2) + (4xh^3 - h^3) + h^4}{h} \\ &= \lim_{h \to 0} \left( 4x^3 - 3x^2 + (6x^2 - 3x + 2)h + (4x - 1)h^2 + h^3 \right) \\ &= 4x^3 - 3x^2 + 4x \end{align*} \) |

|
Table of Derivatives
| Function $(y)$ | Derivative $\left(\frac{dx}{dy}\right)$ |
| $x^n$ | $nx^{n-1}$ |
| $ax^n$ | $anx^{n-1}$ |
| $c=$ constant | $0$ |
| $\sin(x)$ | $\cos(x)$ |
| $\cos(x)$ | $-\sin(x)$ |
| $e^x$ | $e^x$ |
| $\ln (x)$ | $\dfrac{1}{x}$ |
Examples: $ax^n$
• $y= 5x^4$
$\quad \ds \frac{dy}{dx} $ $= (4) 5x^{4-1}$ $= 20x^{3}$
• $y= 124$
$\quad \ds \frac{dy}{dx} =0$
• $y= x^4-x^3+2x^2-1$
$\quad \ds \frac{dy}{dx}$ $= 4x^{4-1}$ $ -\,3x^{3-1}$ $+\,(2)2x^{2-1}$ $-\,0$
$ \qquad \;\;=4x^3-3x^2+4x$
Examples: $a\sin(x),\,b \cos(x)$
• $y= 10 \cos(x)$
$\quad \ds \frac{dy}{dx} $ $= 10\big(-\sin(x)\big)$ $= -10\sin(x)$
• $y= -3 \sin(x)$
$\quad \ds \frac{dy}{dx} = -3 \cos(x)$
• $y= 2\sin(x) + 3 \cos(x)$
$\quad \ds \frac{dy}{dx} =2\cos(x) - 3 \sin(x)$
Examples with $ae^x$
• $y= 2e^x$
$\quad \ds \frac{dy}{dx} $ $= 2e^x$
• $y= -5 e^x$
$\quad \ds \frac{dy}{dx} = -5 e^x$
Examples with $a\ln(x)$
• $y= -3\ln(x)$
$\quad \ds \frac{dy}{dx} $ $= -3\left(\dfrac{1}{x}\right)$ $= -\dfrac{3}{x}$
• $y= 8\ln(x)$
$\quad \ds \frac{dy}{dx} $ $= 8\left(\dfrac{1}{x}\right)$ $= \dfrac{8}{x}$
More examples
• $y= 2x^5 + 3e^x + 5\sin(x)$
$\quad \ds \frac{dy}{dx} $ $= (5)2x^{5-1}$ $+ \,3e^x$ $+\, 5\cos(x)$
$\quad \quad \;\;= 10 x^4 + 3e^x + 5 \cos(x)$
• $y= \dfrac{1}{x^5}+ 7\ln(x)$ $=x^{-5}+ 7 \ln(x)$
$\quad \ds \frac{dy}{dx} $ $= (-5)x^{-5-1}$ $+ \,7\left(\dfrac{1}{x}\right)$
$\quad \quad \;\;= -5 x^{-6} + \dfrac{7}{x}$ $= -\dfrac{5}{x^6} + \dfrac{7}{x}$
More examples
• $y= \sqrt{x}$ $=x^{1/2}$
$\quad \ds \frac{dy}{dx} $ $= \ds\left(\frac{1}{2}\right)x^{1/2-1}$ $= \ds\frac{1}{2}x^{-1/2}$
• $y= \ln\left(x^3\right) $ $=3 \ln\left(x\right)$
$\quad \ds \frac{dy}{dx} $ $= \ds 3 \left(\frac{1}{x}\right)$ $= \ds\frac{3}{x}$
Applications: Turning points
Applications: Turning points
Example 1: Find the turning point of $y = x^2-6x+5.$
$\dfrac{dy}{dx}$ $= 2x^{2-1}$ $ - \,6x^{1-1}$ $+\, 0$
$=2x-6\quad \;$
To find the turning point, let $\dfrac{dy}{dx}=0.$
$2x-6= 0 $ $\;\Ra\; 2x - 6 + 6 = 0+ 6$
$\;\Ra\; \dfrac{2x}{2} = \dfrac{6}{2}$ $\; \Ra \; x=3$
Applications: Turning points
Example 1: Find the turning point of $y = x^2-6x+5.$
When $\dfrac{dy}{dx}=0,$ we found that $x=3.$
Now, for $\,x=3\,$ we have $\,y = (3)^2- 6(3)+5$
$y= 9-18+5$ $=-4\qquad $
Therefore, the turning point is at $\,x=3,\,$ $y = -4$
Applications: Turning points
Example 1: Find the turning point of $y = x^2-6x+5.$
Turning Point: $\,x=3,\,$ $y = -4$
Applications: Turning points
Example 2: Find the turning point(s) of $y = 2x^3+3x^2-12x.$
Applications: Turning points
Example 2: Find the turning point(s) of $y = 2x^3+3x^2-12x.$
$\dfrac{dy}{dx}$ $=6x^2+6x-12$
Let $\dfrac{dy}{dx} = 0.$ So we have $6x^2+6x-12 = 0$
$6(x^2+x-2) = 0$
$6(x+2)(x-1) = 0$
So we obtain $x=-2,$ and $x=1.$
Applications: Turning points
Example 2: Find the turning point(s) of $y = 2x^3+3x^2-12x.$
So we obtain $x=-2,$ and $x=1.$
When $x=-2,$ $\,y = 2(-2)^3+3(-2)^2-12(-2)$ $ = 20$
When $x=1,$ $\,y = 2(1)^3+3(1)^2-12(1)$ $ =-7$
Therefore, the two turning points are:
$P_1:$ $\;x=-2,\,$ $y = 20$
$P_2:$ $\;x=1,\,$ $y = -7\;\;$
Applications: Greatest & Least value
Consider a continuous function $f(x)$ defined on $a\leq x \leq b.$
Applications: Greatest & Least value
Consider a continuous function $f(x)$ defined on $a\leq x \leq b.$
Applications: Greatest & Least value
Consider a continuous function $f(x)$ defined on $a\leq x \leq b.$
The greatest and least values of $f(x)$ will occur:
1. at a turning point ✅
2. at end points of the domain $(x=a,\; x=b)$ ✅
3. where the derivative is not defined (advanced)
Example
Find the greatest and least values of the function $y = x^2 - 6x +4$ where $0\leq x\leq 10.$
We start by finding turning point(s).
So, first compute $\dfrac{dy}{dx}$ $= 2x-6.$
To find turning point, let $\dfrac{dy}{dx}=0.$
$2x-6=0$ $\;\Ra \; x = 3.$
Example
Greatest & Least values: $y = x^2 - 6x +4\;$ on $\;0\leq x\leq 10.$
👉 $x = 3$
We must check also end values at $x=0$ and $x=10$
For $x=0,$ $\;y = (0)^2-6(0)+4$ $\; = 4$
For $x=3,$ $\;y = (3)^2-6(3)+4$ $\; = -5$ $\;$ 👈 Least
For $x=10,$ $\;y = (10)^2-6(10)+4$ $\; = 44$ $\;$ 👈 Greatest
Example
Greatest & Least values: $y = x^2 - 6x +4\;$ on $\;0\leq x\leq 10.$
Applications: Tangent Line
Applications: Tangent Line

|
Slope of the tangent line at $P$ $\dfrac{dy}{dx}= \ds\lim_{h\ra 0}\frac{f(x+h)-f(x)}{h}$ |
Applications: Tangent Line
Find the equation of the tangent line to the function
$y= x^2 -5x\,$ at $\,x=3.$
When $x=3,$ $\;y = (3)^2-5(3)$ $=-6$ $\;\Ra\; P =(3, -6)$
Now, $\dfrac{dy}{dx}$ $\; = 2x-5.\;$ At $x=3,$ we have
$\dfrac{dy}{dx} = 2(3)-5$ $= 1$ $\;\;\Ra\;\; \text{Slope}=m =1$
Applications: Tangent Line
Find the equation of the tangent line to the function
$y= x^2 -5x\,$ at $\,x=3.$
👉 $P =(3, -6)\;\;$ and $\;\;\text{Slope}=m =1$
👉 $y-y_1 = m(x-x_1)$
$\Ra\; y-(-6) = (1)(x-(3))$
$\Ra\; y+6 = x-3$
$\Ra\; y= x-9$
Applications: Tangent Line
Find the equation of the tangent line to the function
$y= x^2 -5x\,$ at $\,x=3.$
👉 $P =(3, -6)\;\;$ and $\;\; y= x-9$
Applications: Tangent Line
Real-world Applications of the Derivative
|
Derivative |
Calculus was developed in the late 1700s
|
Real-world Applications of the Derivative
Instantaneous rate of change: We can easily compute the velocity and acceleration of objects, that is, the derivative of position with respect to time $\left(v(t)=\tfrac{dx}{dt}\right)$ and the derivative of the velocity with respect to time $\left(a(t)=\tfrac{dv}{dt}\right)$, respectively.

Real-world Applications of the Derivative
Optimization: Algorithms in Machine Learning use derivatives (gradient descent), which show the direction and rate of chance of a loss function.
Real-world Applications of the Derivative
Fluid dynamics: Navier-Stokes equations (imcompressible)
Fluid simulation by Amanda Ghassaei

