Linear Algebra & Applications

2201NSC

Affine Transformations

What are affine transformations?

An affine transformation maps points, straight lines and planes while preserving parallelism — parallel lines stay parallel.

Widely used in geometry, computer graphics and vision to map coordinates while keeping geometric relations. Unlike linear transformations, affine transforms can also translate (shift) the space.



What are affine transformations?

This generalisation makes affine transformations particularly useful for:

  • Representing more general geometric deformations
  • Modelling transformations where position changes matter



Affine Transformations

Consider a point $\mathbf x=(x,y).$ A transformation $T: \mathbb R^2 \to \mathbb R^2$ of the form

\( \mathbf{T\left( \mathbf x\right)} = \begin{pmatrix} ax + by + e \\ cx + dy + f \end{pmatrix} \)

where $a,b,c,d,e$ and $f$ are real numbers, is called a two-dimensional affine transformation.



Affine Transformations

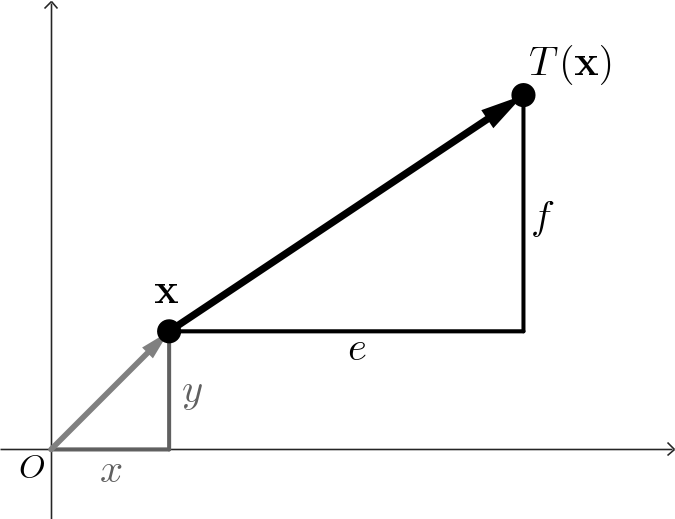
\( \mathbf{T\left( \mathbf x\right)} = \begin{pmatrix} ax + by + e \\ cx + dy + f \end{pmatrix} \)

For example, if $a,d = 1,$ and $b,c=0,$ then we have a pure translation \[ \mathbf{T\left( \mathbf x\right)} = \begin{pmatrix} x + e \\ y + f \end{pmatrix} \]



Mountain landscape

Affine Transformations

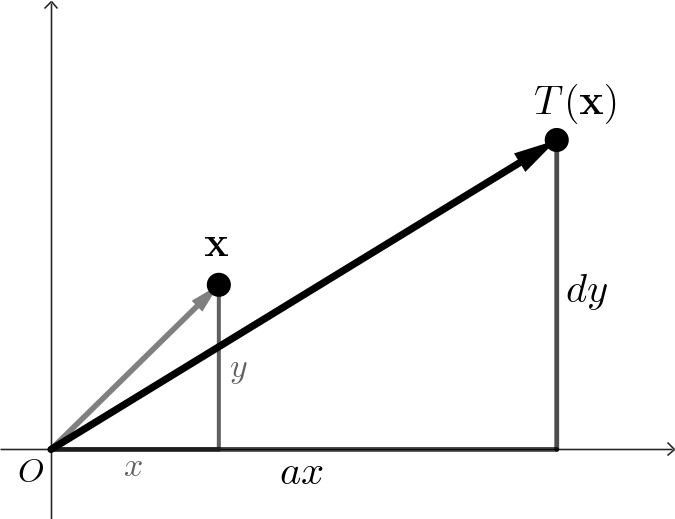
\( \mathbf{T\left( \mathbf x\right)} = \begin{pmatrix} ax + by + e \\ cx + dy + f \end{pmatrix} \)

If $b,c=0$ and $e,f=0;$ then we have a pure scale \[ \mathbf{T\left( \mathbf x\right)} = \begin{pmatrix} ax \\ dy \end{pmatrix} \]



Mountain landscape

Affine Transformations

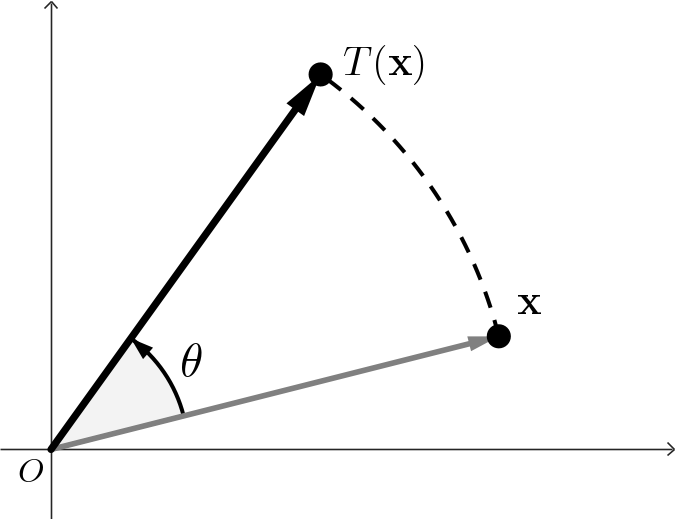
\( \mathbf{T\left( \mathbf x\right)} = \begin{pmatrix} ax + by + e \\ cx + dy + f \end{pmatrix} \)

If $a,d = \cos \theta,$ $b = -\sin \theta,$ $c = \sin \theta,$ and $e,f=0,$ then we have a pure rotation about the origin \[ \small \mathbf{T\left( \mathbf x\right)} = \begin{pmatrix} x\cos\theta -y \sin \theta \\ x\sin \theta + y \cos \theta \end{pmatrix} \]


Mountain landscape

Affine Transformations

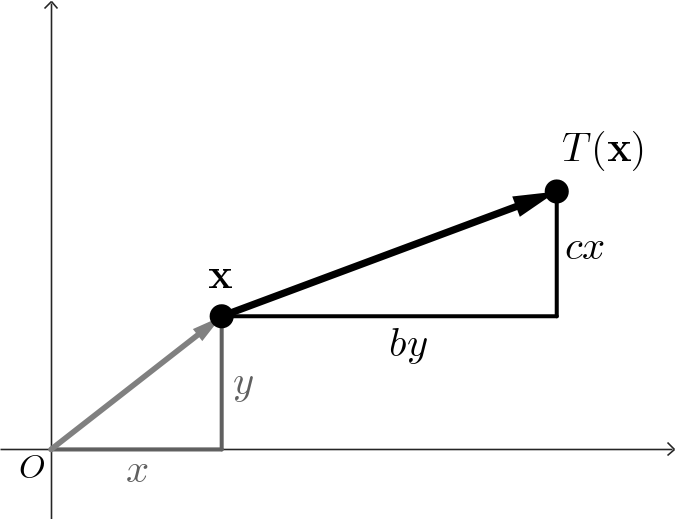
\( \mathbf{T\left( \mathbf x\right)} = \begin{pmatrix} ax + by + e \\ cx + dy + f \end{pmatrix} \)

Finally, if $a,d=1,$ and $e,f=0;$ we have the shear transforms \[ \mathbf{T\left( \mathbf x\right)} = \begin{pmatrix} x+ by \\ y+ cx \end{pmatrix} \]



Mountain landscape

Matrix representation of affine transformations

We know a linear transformation can be written in matrix form

\(T(\mathbf{x}) = \begin{pmatrix} ax + by \\ cx + dy \end{pmatrix} \) \( = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}, \)

Can we do the same with affine transformations? 🤔

No, the problem is the translation❗️




Homogeneous coordinates

To enable affine transformations, such as translation, to be represented using matrix multiplication, we embed these 2D vectors into 3D space using homogeneous coordinates by appending a third coordinate, conventionally set to 1:

\( \begin{pmatrix} x \\ y \end{pmatrix} \) \( \quad \Rightarrow \quad \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}. \)

This third coordinate is typically called \(w\) to distinguish it from the usual \(z\)-coordinate in 3D geometry.


Homogeneous coordinates

Therefore, affine transformations can be written as






Homogeneous coordinates


Affine transformations


Homogeneous coordinates

$\begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix}$ $\begin{pmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{pmatrix}$
Scale

Rotation

$\begin{pmatrix}1 & h_x & 0 \\ h_y & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$ $\begin{pmatrix} 1 & 0 & \Delta x \\ 0 & 1 & \Delta y \\ 0 & 0 & 1 \end{pmatrix}$
Shear Translation


Affine transformations & Fractals

An IFS consists of a finite set of affine transformations \( \{T_1, T_2, \dots, T_n\},\) each of the form:

\( T_i(\mathbf{x}) = A_i \mathbf{x} + \mathbf{t}_i, \)

where \( A_i \) is a \(2 \times 2\) matrix representing a linear transformation (scaling, rotation, or shearing), and \( \mathbf{t}_i \) is a translation vector.



Affine transformations & Fractals

An IFS consists of a finite set of affine transformations \( \{T_1, T_2, \dots, T_n\},\) each of the form:

\( T_i(\mathbf{x}) = A_i \mathbf{x} + \mathbf{t}_i, \)

There are two common approaches for plotting fractals using IFS:

  • Deterministic Algorithm: Apply all transformations to a set of points in each iteration.
  • Random (or Probabilistic) Algorithm: At each step, apply one randomly chosen transformation according to a probability distribution.

Deterministic IFS

We apply the following affine transformations at each iteration:

\( \begin{aligned} T_1(\mathbf x) &= \begin{pmatrix} 0.5 & 0 & 0\\ 0 & 0.5 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}, \\[1ex] T_2(\mathbf{x}) &= \begin{pmatrix} 0.5 & 0 & 0 \\ 0 & 0.5 & 100 \\ 0 & 0 & 1\end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}, \\[1ex] T_3(\mathbf{x}) &= \begin{pmatrix} 0.5 & 0 & 100 \\ 0 & 0.5 & 100 \\ 0 & 0 & 1\end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}. \end{aligned} \)


Deterministic IFS: JavaScript

\( \begin{aligned} T_1(\mathbf x) &= \begin{pmatrix} 0.5 & 0 & 0\\ 0 & 0.5 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}, \end{aligned} \)


\( \begin{aligned} T_2(\mathbf{x}) &= \begin{pmatrix} 0.5 & 0 & 0 \\ 0 & 0.5 & 100 \\ 0 & 0 & 1\end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}, \end{aligned} \)


\( \begin{aligned} T_3(\mathbf{x}) &= \begin{pmatrix} 0.5 & 0 & 100 \\ 0 & 0.5 & 100 \\ 0 & 0 & 1\end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}. \end{aligned} \) 


						
function T1(c) {
  return {
    x: 0.5 * c.x + 0,
    y: 0.5 * c.y + 0,
    r: 0.5 * c.r, // radius
  };
}

function T2(c) {
  return {
    x: 0.5 * c.x + 0,
    y: 0.5 * c.y + 100,
    r: 0.5 * c.r,
  };
}

function T3(c) {
  return {
    x: 0.5 * c.x + 100,
    y: 0.5 * c.y + 100,
    r: 0.5 * c.r,
  };
}

Deterministic IFS: JavaScript


Probabilistic IFS

We apply the following affine transformations, with a given probability for each case:

$ \begin{aligned} T_1(\mathbf{x}) &= \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0.16 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}, \\[1ex] T_2(\mathbf{x}) &= \begin{pmatrix} 0.85 & 0.04 & 0 \\ -0.04 & 0.85 & 1.6 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}, \\[1ex] T_3(\mathbf{x}) &= \begin{pmatrix} 0.2 & -0.26 & 0 \\ 0.23 & 0.22 & 1.6 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}, \\[1ex] T_4(\mathbf{x}) &= \begin{pmatrix} -0.15 & 0.28 & 0 \\ 0.26 & 0.24 & 0.44 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}. \end{aligned} $

Prob
$T_1$ 0.01
$T_2$ 0.85
$T_3$ 0.07
$T_4$ 0.07



Probabilistic IFS

IFS values for a fern

T a b c d e f p
1 0 0 0 0.16 0 0 0.01
2 0.85 0.04 -0.04 0.85 0 1.6 0.85
3 0.2 -0.26 0.23 0.22 0 1.6 0.07
4 -0.15 0.28 0.26 0.24 0 0.44 0.07



Probabilistic IFS: JavaScript

$ \begin{aligned} T_1(\mathbf{x}) &= \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0.16 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{aligned} \mapsto 0.01 $


$ \begin{aligned} T_2(\mathbf{x}) &= \begin{pmatrix} 0.85 & 0.04 & 0 \\ -0.04 & 0.85 & 1.6 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{aligned} \mapsto 0.85 $


$ \begin{aligned} T_3(\mathbf{x}) &= \begin{pmatrix} 0.2 & -0.26 & 0 \\ 0.23 & 0.22 & 1.6 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{aligned} \mapsto 0.07 $


$ \begin{aligned} T_4(\mathbf{x}) &= \begin{pmatrix} -0.15 & 0.28 & 0 \\ 0.26 & 0.24 & 0.44 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{aligned} \mapsto 0.07 $ 


						
let x = 0, y = 0;

function nextPoint() {
  let nextX, nextY, r = random();
  // Apply affine transforms 
  // base on probability distribution
  if (r < 0.01) {
    nextX = 0;
    nextY = 0.16 * y;
  } else if (r < 0.86) {
    nextX = 0.85 * x + 0.04 * y;
    nextY = -0.04 * x + 0.85 * y + 1.6;
  } else if (r < 0.93) {
    nextX = 0.2 * x + -0.26 * y;
    nextY = 0.23 * x + 0.22 * y + 1.6;
  } else {
    nextX = -0.15 * x + 0.28 * y;
    nextY = 0.26 * x + 0.24 * y + 0.44;
  }
  x = nextX;
  y = nextY;
}

Probabilistic IFS: JavaScript